In this mathematics, engineering, and calculus tutorial, we explain how to calculate the minimum and maximum values of functions of two variables. This tutorial is important for a number of real-life engineering and physics problems. The YouTube tutorial accompanying this tutorial is given below. First, we briefly summarize theoretical results, and then, we give several examples at the end of this tutorial.
Theoretical Background
We consider a real-valued function ![]() of two real variables
of two real variables ![]() and
and ![]() . Examples of these functions are given below
. Examples of these functions are given below
(1) 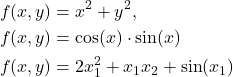
We want to determine (local) minimal and maximal values of such functions.
We assume that the function ![]() is differentiable. Next, let us introduce the following abbreviated notation:
is differentiable. Next, let us introduce the following abbreviated notation:
(2) 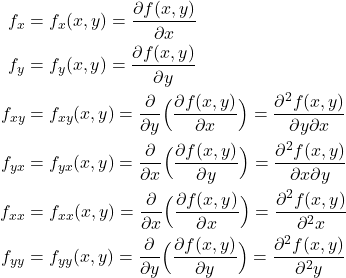
First, we state the following theorem
THEOREM 1 (CRITICAL POINTS AND EXTREME VALUES): If the function ![]() has a (local) minimum or a (local) maximum at the point
has a (local) minimum or a (local) maximum at the point ![]() and
and ![]() , then
, then
(3) ![]()
That is, if the function has a minimum or maximum at the point ![]() , then the partial derivatives
, then the partial derivatives ![]() and
and ![]() evaluated at these points are equal to zero!
evaluated at these points are equal to zero!
The point ![]() is called the critical point or the stationary point if the following two conditions are satisfied:
is called the critical point or the stationary point if the following two conditions are satisfied:
(4) ![]()
Here it should be kept in mind that not all critical points produce minimum or maximum. One example is a saddle point. We will explain this later on when we do several examples. The next theorem gives us conditions for (local) minimum or maximum.
THEOREM 2(SECOND ORDER TEST): Let us suppose that the point ![]() is the critical point of the function
is the critical point of the function ![]() . Define the matrix P of partial derivatives as follows:
. Define the matrix P of partial derivatives as follows:
(5) ![]()
where ![]() ,
, ![]() ,
, ![]() and
and ![]() are defined in (2). Then, let the determinant of
are defined in (2). Then, let the determinant of ![]() be defined by
be defined by
(6) ![]()
where we used the fact that ![]() . Let
. Let ![]() be the value of the determinant of
be the value of the determinant of ![]() evaluated at the critical point
evaluated at the critical point ![]() . Then,
. Then,
- If
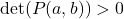 and
and 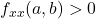 , then the function
, then the function 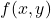 has a local minimum at the critical point
has a local minimum at the critical point 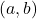 .
. - If
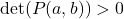 and
and 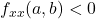 , then the function
, then the function 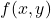 has a local maximum at the critical point
has a local maximum at the critical point 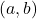 .
. - If
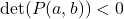 , then the function
, then the function 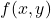 does not have a local minimum at the critical point
does not have a local minimum at the critical point 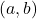 and the function
and the function 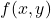 does not have a local maximum at the critical point
does not have a local maximum at the critical point 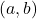 . The point
. The point 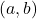 is then called the saddle point of the function
is then called the saddle point of the function 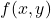 .
.
Here, it is very important to emphasize that if ![]() , then we cannot conclude anything about minimum, maximum, or saddle point. In fact, the function can have a minimum/maximum value or a saddle point. However, we cannot conclude anything about the precise nature of this point.
, then we cannot conclude anything about minimum, maximum, or saddle point. In fact, the function can have a minimum/maximum value or a saddle point. However, we cannot conclude anything about the precise nature of this point.