Calculate Magnitude and Phase of Transfer Functions and Practice Complex Number Transformations – Control Engineering Tutorials – Fusion of Engineering, Control, Coding, Machine Learning, and Science

In this control engineering tutorial, we explain how to calculate the magnitude and phase of transfer functions. Also, the purpose of this tutorial is to practice complex number transformations and algebra that are important for signal processing and control engineering. The YouTube tutorial accompanying this tutorial is given below.

We consider the following transfer function:

(1) $\begin{align*}W(s)=\frac{s+2}{s+3}\end{align*}$

Our goal is to calculate the magnitude and phase of this transfer function. In this tutorial, we assumed a particular form of the transfer function. However, everything explained in this tutorial can easily be generalized to other forms of transfer functions.

The first step when computing the phase and magnitude is to compute the sinusoidal transfer function. This transfer function is obtained by substituting $s$ by $j\omega$ in (1), where $j$ is the imaginary unit and $\omega$ is the angular frequency. As the result of this substitution, we obtain

(2) $\begin{align*}W(j\omega)=\frac{2+j\omega}{3+j\omega}\end{align*}$

After some transformation that we will explain later in this tutorial, this complex number can be represented as follows

(3) $\begin{align*}W(j\omega)=\text{Re}\{W(j\omega) \}+j\text{Im}\{W(j\omega) \}\end{align*}$

where $\text{Re}\{W(j\omega) \}$ and $\text{Im}\{W(j\omega) \}$ are the real and imaginary parts of the sinusoidal transfer functions. The polar form of this complex number is given by

(4) $\begin{align*}W(j\omega)=M(\omega)e^{j\phi}\end{align*}$

where

$M(\omega)$ is the magnitude defined by
(5) $\begin{align*}M(\omega)=\sqrt{\Big( \text{Re}\{W(j\omega) \}\Big)^{2}+\Big(\text{Im}\{W(j\omega) \}\Big)^{2}}\end{align*}$
$\phi$ is the phase is defined by
(6) $\begin{align*}\phi=\arctan \Big(\frac{\text{Im}\{W(j\omega) \}}{\text{Re}\{W(j\omega)\}} \Big) \end{align*}$

There are two approaches for computing the magnitude and phase. The first approach is based on the definitions given by (5) and (6). This approach might be a little bit complex. The second approach is easier and it is based on first transforming the complex numbers in the numerator and denominator of (2) into the polar form.

Let us first present the first approach. We need to compute the real and imaginary parts of (2). We can do that as follows

(7) $\begin{align*}W(j\omega)=\frac{2+j\omega}{3+j\omega}\cdot \frac{3-j\omega}{3-j\omega}=\frac{(2+j\omega)(3-j\omega)}{9+\omega^{2}} =\frac{6+\omega^{2}}{9+\omega^{2}}+j\frac{\omega}{9+\omega^{2}}\end{align*}$

From this expression and from the definition of the magnitude given by the equation (5), we obtain

(8) $\begin{align*}M(\omega) & =\sqrt{\Big( \frac{6+\omega^{2}}{9+\omega^{2}} \Big)^{2} + \Big( \frac{\omega}{9+\omega^{2}} \Big)^{2} }=\sqrt{\frac{36+13\omega^{2}+\omega^{4}}{\big(9+\omega^{2}\big)^{2}}} \\M(\omega) & = \sqrt{\frac{\big(9+\omega^2 \big)\big(4+\omega^2 \big) }{\big(9+\omega^{2}\big)^{2}}}=\sqrt{\frac{4+\omega^2 }{9+\omega^{2}}}\end{align*}$

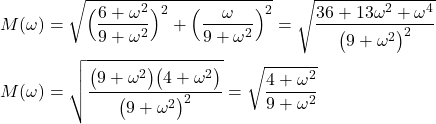
On the other hand, by using (6) and (7), we can compute the phase

(9) $\begin{align*}\phi=\arctan\Big(\frac{\frac{\omega}{9+\omega^{2}}}{\frac{6+\omega^{2}}{9+\omega^{2}}} \Big)=\arctan\Big(\frac{\omega}{6+\omega^{2}} \Big)\end{align*}$

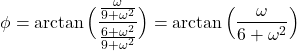
Next, we explain the second approach for computing the magnitude and phase. The idea is to transform the complex numbers in the numerator and denominator of (2) into polar forms. Consequently, we have

(10) $\begin{align*}W(j\omega)=\frac{2+j\omega}{3+j\omega}=\frac{\sqrt{4+\omega^{2}}e^{j\arctan(\frac{\omega}{2})}}{\sqrt{9+\omega^{2}}e^{j\arctan(\frac{\omega}{3})}}=\sqrt{\frac{4+\omega^{2}}{9+\omega^{2}}}e^{j\big( \arctan(\frac{\omega}{2}) - \arctan(\frac{\omega}{3})\big)}\end{align*}$

From this expression, we obtain

(11) $\begin{align*}M(\omega)=\sqrt{\frac{4+\omega^{2}}{9+\omega^{2}}} \\\phi = \arctan(\frac{\omega}{2}) - \arctan(\frac{\omega}{3})\end{align*}$

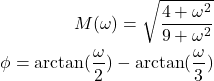
We can observe that the magnitude is equal to the magnitude computed by using the first approach. On the other hand, it seems that the phase is different. However, let us recall this trigonometric formula

(12) $\begin{align*} \arctan(x) - \arctan(y)=\arctan\big(\frac{x-y}{1+xy} \big)\end{align*}$

By using this formula, from (11), we have

(13) $\begin{align*}\phi=\arctan(\frac{\omega}{2}) - \arctan(\frac{\omega}{3})=\arctan \Big(\frac{\frac{\omega}{2} - \frac{\omega}{3} }{1+\frac{\omega}{2}\frac{\omega}{3}} \Big)=\arctan \Big(\frac{\omega}{6+\omega^{2}}\Big)\end{align*}$

This is exactly the phase computed by using the first approach.

admin

You might also like

Some questions for the midterm exam

Test 2

Clear Explanation of the Value Function and Its Bellman Equation – Reinforcement Learning Tutorial