Figure shown below illustrates a Pulse Width Modulation (PWM) signal.
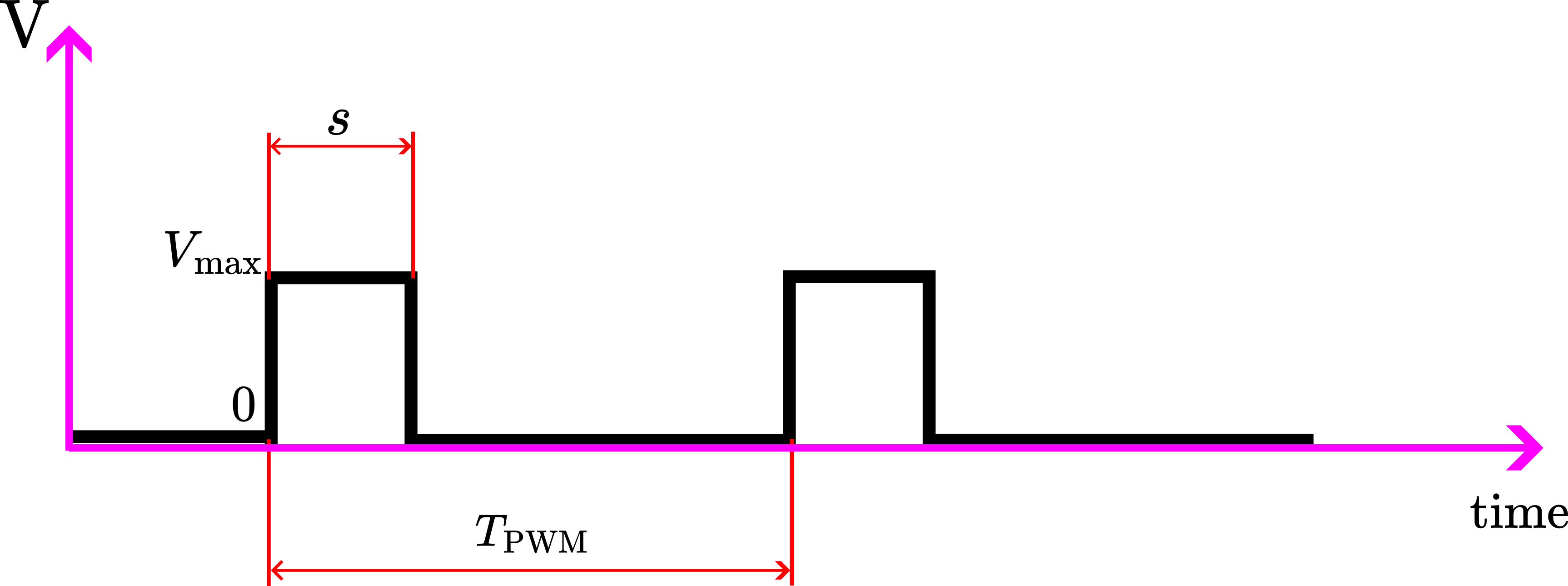
The PWM signal is defined by the following variables
 – length of the pulse
– length of the pulse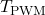 – period of the PWM signal.
– period of the PWM signal. 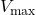 – maximal (voltage) value of the PWM signal.
– maximal (voltage) value of the PWM signal.
The frequency of the PWM signal is
(1) ![]()
The duty cycle is defined by
(2) ![]()
In the STM32 development environment, we select the frequency of the PWM signal by using the three parameters ![]() ,
, ![]() , and
, and ![]() , and the following equation
, and the following equation
(3) ![]()
where
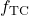 is the frequency of a timer clock of an STM32 microcontroller.
is the frequency of a timer clock of an STM32 microcontroller.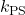 is the prescaler value.
is the prescaler value.-
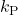 is the period value.
is the period value.
The frequency the time clock ![]() of the clock is measured in MHz. Usually, every STM32 microcontroller has a maximal value. The prescaler value
of the clock is measured in MHz. Usually, every STM32 microcontroller has a maximal value. The prescaler value ![]() is used to downscale the frequency of the time clock. The period value
is used to downscale the frequency of the time clock. The period value ![]() is the final parameter that determines the frequency of the PWM signal.
is the final parameter that determines the frequency of the PWM signal.
In the STM32CubeIDE development environment:
- The period
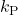 is called “Auto Reload Register” which is abbreviated by ARR. That is,
is called “Auto Reload Register” which is abbreviated by ARR. That is, 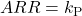 .
.
In the STM32CubeIDE environment, the duty cycle is determined by
(4) ![]()
where ![]() is the Capture/Compare Register (CCR). We select the value of
is the Capture/Compare Register (CCR). We select the value of ![]() in the interval
in the interval ![]() .
.
Let us illustrate this with an example. Let us suppose that we want to generate a PWM signal with the frequency of ![]()
![]() . Let us suppose that the time clock frequency is
. Let us suppose that the time clock frequency is ![]()
![]() . Then, by selecting the prescaler value of
. Then, by selecting the prescaler value of ![]() and the period of
and the period of ![]() , we obtain the desired frequency
, we obtain the desired frequency
(5) ![]()