Z-Transform Introductory Tutorial with Examples of Z-Transform of Unit Impulse Sequence and Unit Step Sequence – Fusion of Engineering, Control, Coding, Machine Learning, and Science

In this digital signal processing and discrete-time control (digital control) tutorial, we will learn

Basic definition of the Z-transform
How to compute the Z-transform of the unit impulse sequence
How to compute the Z-transform of the delayed unit impulse sequence
How to compute the Z-transform of the unit-step sequence

The YouTube video accompanying this post is given below.

Z-transform Definition

Before starting with examples, it is very important to properly understand and memorize the definition of the Z-transform. In this tutorial, we consider sequences that are zero for negative values of the discrete-time instant. Consequently, we consider the unilateral Z-transform defined as follows.

Definition of the unilateral Z-transform of discrete sequences (signals). Let $y[n]$ be a discrete-time sequence: $y[0], y[1], y[2],\ldots$ . Then, the unilateral Z-transform of this sequence is defined by

(1) $\begin{align*}Y(z) &=\mathcal{Z}\big\{ y[n] \big\} \\& =\sum_{n=0}^{\infty} y[n]z^{-n} \\& =y[0]+y[1]z^{-1}+y[2]z^{-2}+y[3]z^{-3}+\ldots\end{align*}$

Here are several important things that should be kept in mind:

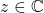$z\in \mathbb{C}$ is a complex number.
The notation 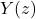$Y(z)$ is the complex variable obtained after the Z-transform of the discrete-time sequence $y[n]$ . That is, the capital letter notation is used to denote the transformed variables that are expressed in the complex z-domain.
The Z-transform transforms signals from the discrete-time domain to the complex $z$ domain. On the other hand, the Laplace transform, transforms continuous-time signals to complex $s$ domain. The Laplace transform is used for continuous-time linear systems. On the other hand, the Z-transform is used for discrete-time systems. That is, what Laplace transform is for continuous-time systems, that is the Z-transform for discrete-time systems.
The notation $\mathcal{Z}\big\{ y[n] \big\}$ is used to denote the actual Z-transform of the discrete sequence $y[n]$ .
The sum in the definition (1) is an infinite sum, and naturally, the question of convergence of such a sum might arise. In this tutorial, we will consider sequences for which the sum in (1) converges. In our future tutorials, we will analyze the convergence in more detail.
Z-transform is a very useful tool for stability analysis, filter design, control system analysis, and design of discrete-time systems. Consequently, if you are working in the field of digital signal processing and real-time control, you have to have a strong understanding of the Z-transform.

In the sequel, we explain how to compute the Z-transform for several elementary and commonly used sequences in digital signal processing. In the second part of this tutorial, we will explain how to compute the Z-transform for other types of sequences.

Z-transform of the unit impulse sequence

The unit impulse sequence is a fundamental sequence in signal processing. It is often denoted by $\delta [n]$ and is defined as follows

(2) $\begin{align*}\delta[n] = \left\{ \begin{array}{ll} 1 & , \;\; n=0 \\ 0 & , \;\; n \ne 0 \end{array} \right.\end{align*}$

Since this sequence is zero for $n<0$ , we use the unilateral Z-transform. We have

(3) $\begin{align*}\mathcal{Z}\big\{ \delta[n] \big\}=\sum_{n=0}^{\infty} \delta[n]z^{-n}=\delta [0]+\delta[1]z^{-1}+\delta [2]z^{-2}+\delta [3]z^{-3}+\ldots\end{align*}$

Since, $\delta[0]=1$ , and $\delta[1]=0$ , $\delta[2]=0$ , $\delta[3]=0$ , … , we have

(4) $\begin{align*}\mathcal{Z}\big\{ \delta[n] \big\}=\sum_{n=0}^{\infty} \delta[n]z^{-n}=1+0\cdot z^{-1}+0\cdot z^{-2}+0\cdot z^{-3}+\ldots\end{align*}$

Consequently, we have

(5) $\begin{align*}\mathcal{Z}\big\{ \delta[n] \big\}=1\end{align*}$

Z-transform of the delayed unit impulse sequence

The delayed unit impulse sequence is defined by the following equation

(6) $\begin{align*}\delta[n-m] = \left\{ \begin{array}{ll} 1 & , \;\; n=m \\ 0 & , \;\; n \ne m \end{array} \right.\end{align*}$

We have

(7) $\begin{align*}\mathcal{Z}\big\{ \delta[n-m] \big\} & =\sum_{n=0}^{\infty} \delta[n-m]z^{-n} \\& =\delta [-m]+\delta[1-m]z^{-1}+\delta [2-m]z^{-2}+\delta [3-m]z^{-3} \\& +\ldots+ \delta[m-m]z^{-m}+\delta[m-m+1]z^{-m+1}+\ldots\end{align*}$

(8) $\begin{align*}\mathcal{Z}\big\{ \delta[n-m] \big\} & =\sum_{n=0}^{\infty} \delta[n-m]z^{-n} \\& =\delta [-m]+\delta[1-m]z^{-1}+\delta [2-m]z^{-2}+\delta [3-m]z^{-3} \\& +\ldots+ \delta[0]z^{-m}+\delta[+1]z^{-m+1}+\ldots\end{align*}$

We have that $\delta[0]=1$ , and all other terms are equal to zero. By using this fact, from (8) we have

(9) $\begin{align*}\mathcal{Z}\big\{ \delta[n-m] \big\} & =z^{-m}\end{align*}$

This is actually a very important result that is often used in digital signal processing. The Z-transform of a delayed unit impulse if $z^{-m}$ , where, $m$ is the actual delay. From here, we have a very important interpretation of the $z$ complex variable. Namely, when we multiply a signal $Y(z)$ by the negative $m$ the power of $z$ , that is by $z^{-m}$ , in the time domain, we will obtain the delayed signal $y[n-m]$ . That is, the time equivalent of $z^{-m}Y(z)$ is $y[n-m]$ . This is a very important important result.

Z-transform of the unit step sequence

The unit step sequence is another very important sequence or signal used in digital signal processing and digital control theory. It is usually denoted by $u[n]$ and is defined as follows

(10) $\begin{align*}u[n] = \left\{ \begin{array}{ll} 1 & , \;\; n \ge 0 \\ 0 & , \;\; n < 0 \end{array} \right.\end{align*}$

That is, this sequence is equal to $1$ for zero and positive values of $n$ . This is a classical step signal used to test the response of dynamical systems. The Z-transform of the unit step sequence is:

(11) $\begin{align*}\mathcal{Z}\big\{ u[n] \big\} & =\sum_{n=0}^{\infty} u[n] z^{-n}=u[0]+u[1]\cdot z^{-1}+u[2]\cdot z^{-2}+u[3]\cdot z^{-3}+\ldots \\& =1+1\cdot z^{-1}+1\cdot z^{-2}+1\cdot z^{-3}+\ldots \\& =\sum_{n=0}^{\infty} z^{n}\end{align*}$

Next, we will determine the closed analytical form of the Z transform of the unit step sequence. The last equation in (11), is very similar to the classical geometric series of real numbers. In fact, the formulas for the sum and for the sum of $N$ first geometric series are mathematically equivalent to the formulas for the last equation of (11). Let us consider the following finite sum of the first $N$ terms of the infinite series given by the last equation in (11).

(12) $\begin{align*}S_{N}=z^{0}+z^{-1}+z^{-2}+\ldots +z^{-(N-1)}\end{align*}$

Similarly to the sum of the first $N$ terms of the geometric series, the sum $S_{N}$ is equal to

(13) $\begin{align*}S_{N}=\frac{1-z^{-N}}{1-z^{-1}}\end{align*}$

where $z^{-1}$ can be interpreted as the common ratio. The common ratio is the ratio of the two subsequent elements in a geometric series, for example, the second element in the series given by the last equation in (11) is $z^{-1}$ , and the third element is $z^{-2}$ . The ratio $z^{-2}/z^{-1}$ is equal to $z^{-1}$ , and the same is valid for all other subsequent entries of the series.

Now, if we let $N$ approach infinity, and under the assumption that the modulus of the complex number $z$ , that is $|z|$ , is larger than 1, from (13), we obtain

(14) $\begin{align*}S_{\infty}=\frac{1}{1-z^{-1}}\end{align*}$

By combining the last equation in (11) with (14), we obtain

(15) $\begin{align*}\mathcal{Z}\big\{ u[n] \big\} =\sum_{n=0}^{\infty} z^{n} =S_{\infty}=\frac{1}{1-z^{-1}}\end{align*}$

(16) $\begin{align*}\mathcal{Z}\big\{ u[n] \big\} = \frac{1}{1-z^{-1}}=\frac{z}{z-1}\end{align*}$

and that is the final expression for the Z-transform of the unit step sequence.

Z-transform Definition

Z-transform of the unit impulse sequence

Z-transform of the delayed unit impulse sequence

Z-transform of the unit step sequence

admin

You might also like

How to Sketch Bode Diagrams by Hand – First Order Transfer Function Without Zeros

How to Check the Stability of State-Space Models in MATLAB – Several Approaches Thoroughly Explained – Control Engineering Tutorial

Simple Discrete-time Model of Mobile Robot for Localization, SLAM, and Dead Reckoning