Tutorial on Matrix Operations in Python by Using Numpy Matrix Libary

In this Python and numerical computing tutorial, we explain how to define matrices in Python and how to perform basic matrix operations in Python. To perform the basic matrix operations, we use the NumPy library. In particular, we explain how to

1. Define matrices in Python by using NumPy.
2. Define zero matrices and identity matrices in Python by using NumPy.
3. How to access matrix entries, and how to access rows and columns.
4. How to retrieve the matrix shapes and dimensions.
5. How to perform matrix operations such as addition, multiplication, and transpose.
6. How to define block matrices in Python by using NumPy.
7. How to invert matrices.
8. How to load and save matrices to from files in NumPy.

The YouTube tutorial accompanying this tutorial is given below.

The first step is to install the NumPy library. We can do that by typing “pip install numpy” in the command window.

First, let us define the matrices. For example, let us consider the following matrices

(1)  

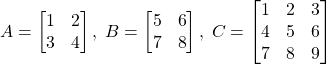
The following Python script will import the Numpy library as “np” (“np” is just an alias we selected for Numpy ). Then, it will define the matrices by using “np.array()” function.

import numpy as np 

#defining matrices
A=np.array([[1,2],[3,4]])
B=np.array([[5,6],[7,8]])
C=np.array([[1,2,3],[4,5,6],[7,8,9]])

We define the matrices row-wise, using the function “np.array()”. The rows are enclosed by “[ ]”, and the rows are separated by commas.

Another useful technique for defining matrices is to directly specify the data type while defining the matrices. This might be necessary if we want to transfer matrix data from Python to some other programming language, such as for example MATLAB. We can explicitly define the data type of matrix entries as follows

G=np.array([[1, 2, 3], [4, 5, 6]], np.double)

We can investigate the data type by using “dtype” function as follows

G.dtype

We can define zero matrices and identity matrices as follows

# zero and identity matrices
I4=np.identity(4)
Z4=np.zeros(shape=(4,4))

We can access rows, columns, and blocks of matrices using the following commands that are similar to MATLAB basic operations

# first row 
C[0,:]

# first column
C[:,0]

# first two rows

C[0:2,:]

# sub-block
C[0:2,0:2]

 C[-2:,-2:]

Python enumerates array entries from 0 and not from 1. Consequently, the notation C[0,0], corresponds to the (1,1) entry of the matrix C. Matrix dimensions can be obtained using the following Python script.

# get the number of rows and columns 
A.shape

#row number directly
A.shape[0]

#column number directly
A.shape[1]

There are two approaches for computing matrix transposes.

#transpose 
A.T
np.transpose(A)

We can add (subtract) two matrices as follows.

#add two matrices 
D=A+B

The multiplication operator “*” in NumPy denotes element-wise multiplication and is not the matrix multiplication operator. You can convince yourself by typing

#multiply two matrices

D=A*B # THIS IS NOT MATRIX MULTIPLICATION - THIS IS ELEMENT-WISE MULTIPLICATION

There are at least two ways for correctly performing matrix multiplication. The first one is given below

Dcorrect=A.dot(B) # THIS IS CORRECT WAY FOR MULTIPLYING TWO MATRICES

Block matrices can be defined as follows

# block matrices

BlockMatrix=np.block([
        [np.zeros(shape=(3,3)), np.identity(3)],
        [-np.identity(3),                   -C]
        ])

Matrix inversion is performed as follows.

# matrix inversion
from numpy.linalg import inv

Ainv=inv(A)

# check the result
Ainv.dot(A)
A.dot(Ainv)

Next, let us learn how to save and load matrices to and from files in Python. There are at least two ways to perform these operations. The first approach is to save the matrix in a “.mat” format. This format is a MATLAB format for saving matrices. We will define a matrix, and on the basis of this matrix, we will define a dictionary that will be saved as the “.mat” file type. Then, we will load the matrix from the file.

# save and load matrices from files

# using MATLAB ".mat" format
from scipy.io import savemat
from scipy.io import loadmat

G=np.array([[1, 2, 3], [4, 5, 6]], np.double)
G.dtype

# define a dictionary
mdic ={'G': G}
# save the matrix to file
savemat("matlab_matrix.mat", mdic)
#load matrix from file
matrix = loadmat('matlab_matrix.mat')
loadedG=matrix['G']

Another way for storing matrices is to store them directly using the Numpy “save()” function. We can load the matrices using the “load()” function. The matrices are saved in a file with the extension “.npy”.

# save and load the matrix using numpy save 

np.save('numpy_matrix.npy', G)
G2 = np.load('numpy_matrix.npy')
print(G == G2)