In this post, we explain how the expected value of the state vector and state covariance matrix of linear dynamical systems are propagated in discrete-time. These equations, together with the equations describing the recursive least squares method which are derived in our previous post, are important for deriving the Kalman filter equations.
Linear Dynamical System Affected by the Process Noise (Disturbances)
We are considering the following state equation
(1) ![]()
where
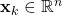 is the state vector
is the state vector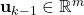 is the control input vector
is the control input vector 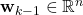 is the disturbance or process noise vector. We assume that
is the disturbance or process noise vector. We assume that 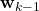 is Gaussian, zero-mean, white noise with the covariance matrix given by
is Gaussian, zero-mean, white noise with the covariance matrix given by ![Rendered by QuickLaTeX.com Q_{k}=E[\mathbf{w}_{k}\mathbf{w}_{k}^{T}]](https://aleksandarhaber.com/wp-content/ql-cache/quicklatex.com-266e7fa5fa9769934ad70b1a27d1a31b_l3.png) , where
, where ![Rendered by QuickLaTeX.com E[\cdot]](https://aleksandarhaber.com/wp-content/ql-cache/quicklatex.com-3941b329206b0baa01fad23b819cc5f7_l3.png) is the mathematical expectation operator.
is the mathematical expectation operator. 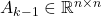 and
and 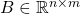 are state and input matrices.
are state and input matrices.
A few comments are in order. If the system is time-invariant, then the matrices ![]() ,
, ![]() , and
, and ![]() are constant, that is
are constant, that is ![]() ,
, ![]() , and
, and ![]() . The process disturbance vector
. The process disturbance vector ![]() can take into account unmodeled dynamics that is simply assumed as a stochastic disturbance, and/or stochastic disturbances affecting the state vector.
can take into account unmodeled dynamics that is simply assumed as a stochastic disturbance, and/or stochastic disturbances affecting the state vector.
State Vector Expectation Propagation
Let us apply the expectation operator to the equation (1), as the result, we obtain
(2) ![]()
For notation brevity, we introduce the following notation
(3) ![]()
Taking into account that ![]() (the disturbance vector is zero mean), we obtain our final equation for state vector expectation propagation over discrete-time:
(the disturbance vector is zero mean), we obtain our final equation for state vector expectation propagation over discrete-time:
(4) ![]()
State Covariance Matrix Propagation
We define the state covariance matrix as follows
(5) ![]()
Consequently, we first need to expand this expression
(6) ![]()
and then compute the expectation of every term in that expression. By substituting the equations (1) and (4) in (10), we obtain
(7) 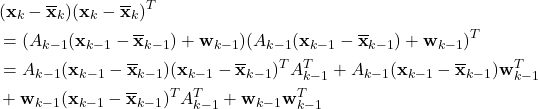
Since ![]() is uncorrelated with
is uncorrelated with ![]() , we have
, we have
(8) ![Rendered by QuickLaTeX.com \begin{align*}E[A_{k-1}(\mathbf{x}_{k-1}-\overline{\mathbf{x}}_{k-1})\mathbf{w}_{k-1}^{T}]=0 \\E[\mathbf{w}_{k-1}(\mathbf{x}_{k-1}-\overline{\mathbf{x}}_{k-1})^{T}A_{k-1}^{T}]=0\end{align*}](https://aleksandarhaber.com/wp-content/ql-cache/quicklatex.com-718487f6340e86c492ddc9856a12d4f9_l3.png)
Also, we have
(9) ![]()
(10) ![]()
By using these expressions, and by taking the expectation of (7), we obtain the final equation for the propagation of the state covariance matrix
(11) ![]()