The Correct Definition of the Fluid Flow Rate and Average Fluid Flow Rate – Derivation of the Formula Q=V*A – Fusion of Engineering, Control, Coding, Machine Learning, and Science

In this fluid dynamics and fluid mechanics tutorial, we provide a correct and intuitive definition and explanation of the fluid flow rate. Also, in this tutorial, we derive the famous equation for the flow rate that says that the flow rate is the product of the fluid flow velocity and the cross-section area through which the fluid passes. In the next tutorial given here, we provide an intuitive and correct explanation of the continuity equation.

The main motivation for creating this lecture comes from the fact that online you will often find incorrect or only partially correct definitions of the fluid flow rate or the definition is stated by using very complex mathematics, such double integrals and multivariable calculus. Consequently, most of the students do not obtain the correct and intuitive understanding of this important concept that is essential for the development of other definitions and concepts in fluid dynamics. In reality, with only the knowledge of the basic calculus, one can easily understand the concept of the volumetric fluid flow rate. The YouTube video accompanying this webpage is given below.

Definition of Fluid Flow Rate

Here, we will state the correct definition and give a proper physical explanation of the fluid (volumetric) flow rate. Consider the figure shown below.

Figure 1: Figure used to define the flow rate.

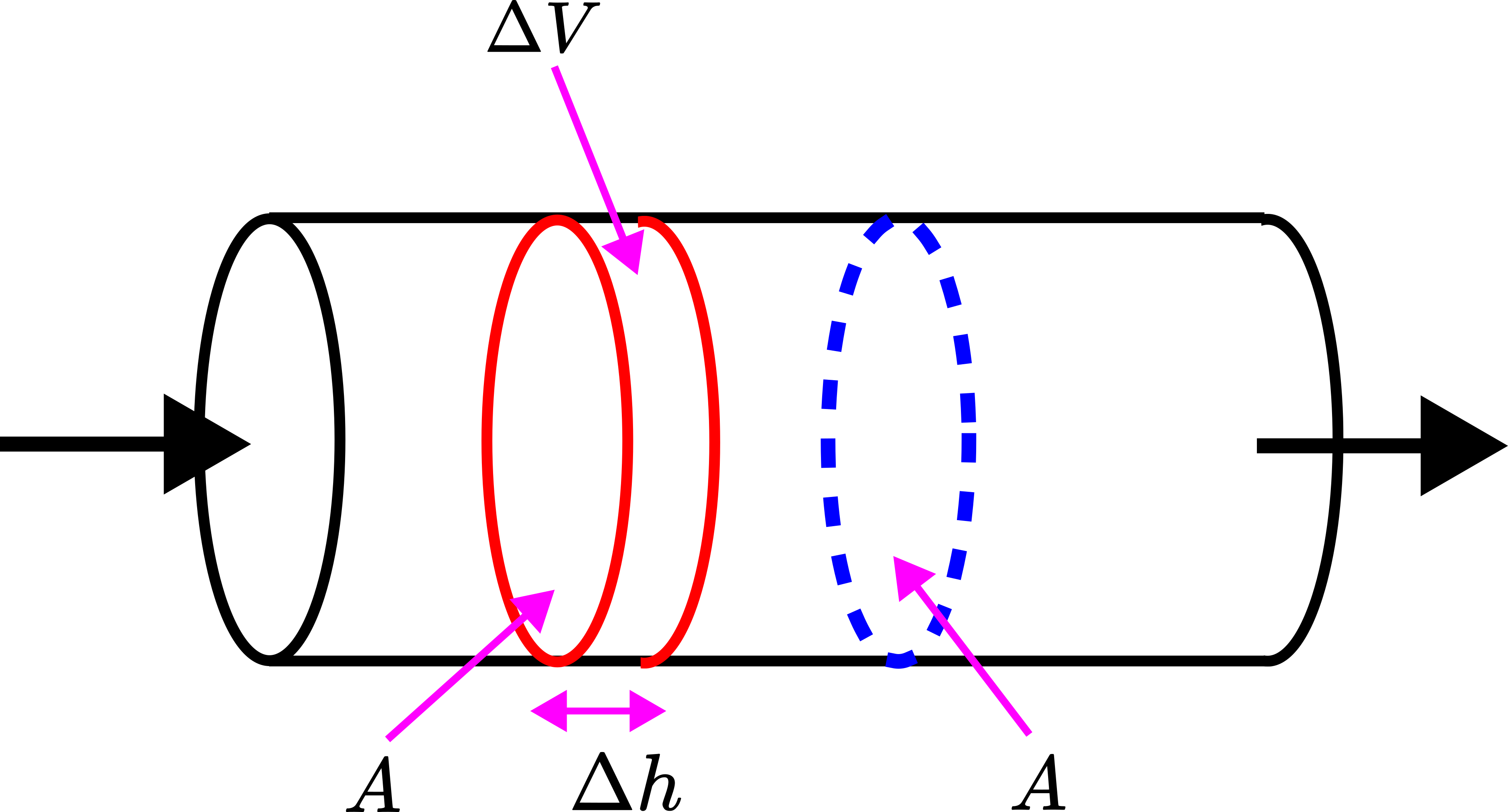
This figure shows a section of a cylindrical pipe. The fluid flow direction is from left to right. The first thing that we need to do is to identify a volume of fluid. In the figure shown above the volume of fluid is a red cylinder. Next, we need to identify a cross-section area of the fluid flow.

Next, consider the figure shown below. At the time instant $t$ , the volume of fluid enters the cross-section area. At the time instant $t+\Delta t$ , the volume of fluid exists the cross-section area. That is, it takes $\Delta t$ amount of time for the volume of fluid to pass through the cross section area

The average (volumetric) fluid flow rate is the volume of the fluid that passes or flows through the cross-section area during the time interval $\Delta t$ .

Let us now mathematically formulate this definition. Let the volume of fluid be denoted by $\Delta V$ . Then, let the cross-section area be denoted by $A$ . This is shown in the figure below.

Then, the average flow rate, denoted by $Q_{\text{AVG}}$ , through the cross-section area is

(1) $\begin{align*}Q_{\text{AVG}}=\frac{\Delta V}{\Delta t}\end{align*}$

The unit of $Q_{\text{AVG}}$ is $m^{3}/s$ (cubic meters per second). From the figure shown above, it follows that

(2) $\begin{align*}\Delta V =\Delta h \cdot A\end{align*}$

By substituting (2) in (1), we obtain

(3) $\begin{align*}Q_{\text{AVG}}=\frac{\Delta h \cdot A}{\Delta t} = \frac{\Delta h}{\Delta t}\cdot A\end{align*}$

On the other hand, the distance that any cross-section of the volume of fluid travels during the time interval $\Delta t$ is $\Delta h$ . Consequently, the term

(4) $\begin{align*}\frac{\Delta h}{\Delta t}\end{align*}$

is the average velocity of the volume of fluid. That is, we have

(5) $\begin{align*}v_{\text{AVG}}=\frac{\Delta h}{\Delta t}\end{align*}$

By substituting (5) in (3), we have

(6) $\begin{align*}Q_{\text{AVG}}=v_{\text{AVG}}\cdot A\end{align*}$

That is, the average flow rate is the product of the average velocity $v_{\text{AVG}}$ of the volume of fluid and the cross-section area $A$ .

Now, that we know how to properly define the average flow rate, we can define the instantaneous flow rate. The instantaneous flow rate is defined by

(7) $\begin{align*}Q= \lim_{\Delta t \rightarrow 0}Q_{\text{AVG}}=\limit_{\Delta t \rightarrow 0} \frac{\Delta h}{\Delta t} \cdot A\end{align*}$

Taking into account that

(8) $\begin{align*}\lim_{\Delta t \rightarrow 0} \frac{\Delta h}{\Delta t} \end{align*}$

is actually the definition of the instantaneous velocity $v$ , that is

(9) $\begin{align*}v=\lim_{\Delta t \rightarrow 0} \frac{\Delta h}{\Delta t} \end{align*}$

we can write the expression for the instantaneous flow rate as

(10) $\begin{align*}Q= v \cdot A\end{align*}$

That is, the instantaneous flow rate is defined as the product of the instantaneous velocity $v$ of the volume of fluid and the cross-section area $A$ through which the fluid flows. We usually omit the word “instantaneous”, and we refer to the instantaneous flow rate simply as the flow rate or the volumetric flow rate.

Definition of Fluid Flow Rate

admin

You might also like

Introduction to Rotation Matrices in Robotics

Easy Explanation of Batch Gradient Descent Method with Python Implementation

Arduino-ROS Interface with Python – Send Messages From Python/ROS to Arduino and Receive Messages Back – Tutorial