Solve Optimization Problems using MATLAB- Disciplined Approach Using fmincon() – Fusion of Engineering, Control, Coding, Machine Learning, and Science

In this optimization tutorial, we explain how to solve multi-variable optimization problems in MATLAB. We use the MATLAB function fmincon(). We explain how to define the problem, how to solve it, and how to provide constraints and gradients. Gradients are necessary if we want to speed up the computations. We first explain the basic ideas on a least-squares problem and later on, we show how to solve a more complex problem. The YouTube video tutorial accompanying this tutorial is given below

A least-squares problem

Let us first start with a simple problem for which we know how to compute the solution analytically. We start with such a problem since we want to verify the MATLAB solution.

Consider the cost function:

(1) $\begin{align*}J(x_{1},x_{2})=(y_{1}-a_{11}x_{1}-a_{12}x_{2})^{2}-(y_{2}-a_{21}x_{1}-a_{22}x_{2})^{2}\end{align*}$

where $x_{1},x_{2}\in \mathbb{R}$ are the optimization variables, and $y_{1},y_{2},a_{11},a_{12},a_{21},a_{22}\in \mathbb{R}$ are the known quantities. Our goal is to solve the following optimization problem

(2) $\begin{align*}\min_{x_{1},x_{2}} J(x_{1},x_{2})\end{align*}$

This optimization problem is a least-squares problem. It has many practical applications. It is extensively used for sensor calibration, curve fitting, signal processing, control system design, etc.

There are at least two ways for minimizing the cost function (2). The first approach is to compute the partial derivatives and to set them to zero:

(3) $\begin{align*}\frac{\partial J}{\partial x_{1}}=-2a_{11}(y_{1}-a_{11}x_{1}-a_{12}x_{2})-2a_{21}(y_{2}-a_{21}x_{1}-a_{22}x_{2})=0 \\ \frac{\partial J}{\partial x_{2}}=-2a_{12}(y_{1}-a_{11}x_{1}-a_{12}x_{2})-2a_{22}(y_{2}-a_{21}x_{1}-a_{22}x_{2})=0 \\\end{align*}$

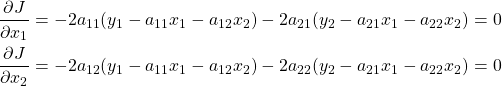
Let us introduce the matrices and vectors:

(4) $\begin{align*}A=\begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix}, \mathbf{y}=\begin{bmatrix}y_{1} \\ y_{2} \end{bmatrix}, \mathbf{x}=\begin{bmatrix} x_{1} \\ x_{2} \end{bmatrix}\end{align*}$

Using the basic rules of matrix-vector calculus, we can rewrite the system of equations (3) as follows

(5) $\begin{align*}\begin{bmatrix} \frac{\partial J}{\partial x_{1}} \\ \frac{\partial J}{\partial x_{2}} \end{bmatrix}=-2A^{T}(\mathbf{y}-A\mathbf{x})=0\end{align*}$

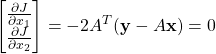
where $A^{T}$ is the matrix transpose. From the last equation, we obtain

(6) $\begin{align*}A^{T}A\mathbf{x}=A^{T}\mathbf{y}\end{align*}$

The system of equations (6) is often referred to as the normal equations. Assuming that the matrix $A^{T}A$ is invertible, the solution is given by

(7) $\begin{align*}\mathbf{x}=(A^{T}A)^{-1}A^{T}\mathbf{y}\end{align*}$

That is, due to the particular form of the cost function (10), we can find the solution in the closed form. Let us now solve the optimization problem using the MATLAB solver. We will use the equation (7) to compare the MATLAB solution with the “exact” solution.

First, we define a MATLAB function having the following form:

function [solution,fval,exitflag,output]=minimize_cost_function(A,y,x0)

% summary of the optimization problem-general form
% fmincon attempts to solve problems of the form:
%     min J(x)  subject to:  Aineq*x  <= Bineq, Aeq*x  = Beq (linear constraints)
%      x                    C(x) <= 0, Ceq(x) = 0   (nonlinear constraints)
%                               lb <= x <= ub        (bounds)


Aineq=[];
Bineq=[];
Aeq=[];
Beq=[];
lb=[];
ub=[];

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% keyboard
% algorithm can be 'interior-point', 'SQP','active set', and 'trust region reflective'
% set the options
options = optimoptions(@fmincon,'Algorithm','interior-point','SpecifyObjectiveGradient',false,'Display','iter','MaxFunctionEvaluations',10000,'UseParallel',true,'OptimalityTolerance',1.0000e-8, 'StepTolerance',1.0000e-8)

[solution,fval,exitflag,output] = fmincon(@(x)cost_function(x),x0,Aineq,Bineq,Aeq,Beq,lb,ub,[],options);


function J=cost_function(x)
    % notice that this function can access the arguments of the function
    % minimize_cost_function()
    
    J=norm(y-A*x,2)^2;
    
end

end

It is important to save this function in a new folder, and to name this function ” minimize_cost_function.m”. That is, the name of the function should correspond to the name used in the function declaration/definition. On the code line 1, we can see that this function returns several variables. The solution to the optimization problem is stored in “solution”. We can use the code lines 10-15 to define the constraints for the optimizer. However, in our case, we are considering an unconstrained problem, so these constraints are left empty. The code line 21 defines the options for the solver. We can select an algorithm, set the optimization tolerances, or even tell the optimizer to use the gradient of the cost function. We we the option “Display” to “iter” to monitor and plot the optimization progress. The first option “@fmincon” tells MATLAB that we plan to use the build-in “fmincon” function to solve the problem. We use the code line 23 to solve the problem. The first argument of the fmincon() function is “@(x)cost_function(x)”. This argument is used to tell fmincon() that the cost function is defined in the function “cost_function(x)” that is defined on the code lines 26-32. The other arguments are used to define the initial solution “x0” and constraints.

After saving the function “minimize_cost_function.m” in a folder and after adding this folder to the MATLAB path (do not forget to do this!), we can call this function from another MATLAB script given below

% generate A coefficient matrix and y vector
A=randn(10,10);
y=rand(10,1)

% initial guess for the solution
x0=randn(10,1)

% solve the problem
[solution,fval,exitflag,output]=minimize_cost_function(A,y,x0)

% compute the least-squares solution
exact_solution=inv(A'*A)*A'*y

% compare the computed solution with the exact solution
norm(solution-exact_solution,2)/norm(exact_solution,2)

A few comments are in order. The code lines 2-6 are used to define the coefficient matrix A, the vector $\mathbf{y}$ and an initial solution guess. Notice that we choose these quantities as random matrices/vectors (type “help rand” and “help randn” to see basic descriptions of these functions). The code line 9 is used to solve the problem. We use this code line to call the function “minimize_cost_function” that is stored in the MATLAB path, so you can call this function from another script. The code line is used to compute the least-squares solution defined by the equation (7). Finally, the code line 15 is used to compare “solution” with the exact (least-squares) solution. The relative error is below 6%.

A more complex problem

Let us know write the MATLAB code that will solve the following optimization problem:

(8) $\begin{align*}min_{x_{1},x_{2}, x_{3}} J(x_{1},x_{2},x_{3}) \\ \\\text{subject to:}\;\; -100 \le x_{1} \le 100, \;\; -200 \le x_{2} \le 200, \;\;\; -300 \le x_{3} \le 300\end{align*}$

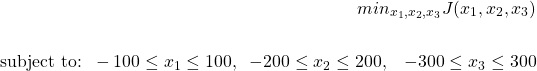
where

(9) $\begin{align*}J(x_{1},x_{2}, x_{3})=\left\|\begin{bmatrix} 10-x_{1}\sin(x_{2}) \\ 100 -x_{2}^{3}-x_{3}^{5}\\ 23-x_{1}^{2}-x_{2}-x_{3} \end{bmatrix} \right\|_{2}^{2}\end{align*}$

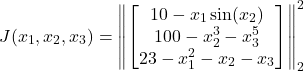
Notice that now, in sharp contrast to the previously considered least-squares problem, we have constraints. The cost function (9), can also be written as follows:

(10) $\begin{align*}J(x_{1},x_{2}, x_{3})=(10-x_{1}\sin(x_{2}))^{2}+(100 -x_{2}^{3}-x_{3}^{5})^{2}+(23-x_{1}^{2}-x_{2}-x_{3})^2\end{align*}$

The modified function “minimize_cost_function” takes the following form:

function [solution,fval,exitflag,output]=minimize_cost_function(x0)

% summary of the optimization problem-general form
% fmincon attempts to solve problems of the form:
%     min J(x)  subject to:  Aineq*x  <= Bineq, Aeq*x  = Beq (linear constraints)
%      x                    C(x) <= 0, Ceq(x) = 0   (nonlinear constraints)
%                               lb <= x <= ub        (bounds)


Aineq=[];
Bineq=[];
Aeq=[];
Beq=[];
lb=[-100; -200; -300];
ub=[100; 200; 300];

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% keyboard
% algorithm can be 'interior-point', 'SQP','active set', and 'trust region reflective'
% set the options
options = optimoptions(@fmincon,'Algorithm','interior-point','SpecifyObjectiveGradient',false,'Display','iter','MaxFunctionEvaluations',10000,'UseParallel',true,'OptimalityTolerance',1.0000e-12, 'StepTolerance',1.0000e-10)

[solution,fval,exitflag,output] = fmincon(@(x)cost_function(x),x0,Aineq,Bineq,Aeq,Beq,lb,ub,[],options);


function J=cost_function(x)
    % notice that this function can access the arguments of the function
    % minimize_cost_function()
    F=[10-x(1)*sin(x(2)); 100-x(2)^(3)-x(3)^(5); 23-x(1)^(2)-x(2)-x(3)];
    
    J=norm(F,2)^2;
    
end

end

We briefly comment upon the main changes made with respect with the previous function version. The code lines 14-15 are used to incorporate the constraints of the optimization problem (8). The code lines 29-31 are used to code the cost function. This function is called from the following script.

% initial guess for the solution
x0=randn(3,1)

% solve the problem
[solution,fval,exitflag,output]=minimize_cost_function(x0)

F_initial=[10-x0(1)*sin(x0(2)); 100-x0(2)^(3)-x0(3)^(5); 23-x0(1)^(2)-x0(2)-x0(3)];

norm(F_initial,2)^2

F=[10-solution(1)*sin(solution(2)); 100-solution(2)^(3)-solution(3)^(5); 23-solution(1)^(2)-solution(2)-solution(3)];

norm(F,2)^2

In this case, we only need to specify the initial condition. The code lines 7-13 are used to verify that the cost function is optimized. In our simulation, the initial value of the cost function, stored in “F_initial” is 1.0424e+04. The final value of the cost function, stored in “F” is 27.8236.

A least-squares problem

A more complex problem

admin

You might also like

Eigen C++ Matrix Library Tutorial – Saving and Loading Data In and From CSV Files

Review of Torsion

Import *.csv and *.txt Numerical Files and Data in MATLAB

Import .csv and .txt Numerical Files and Data in MATLAB