The polar moment of inertia is used to compute the maximal shear stress when an element is subject to torsional load. Consequently, it is important to know how to calculate the polar moment of inertia for simple geometries.
Consider a circle shown in the figure below.
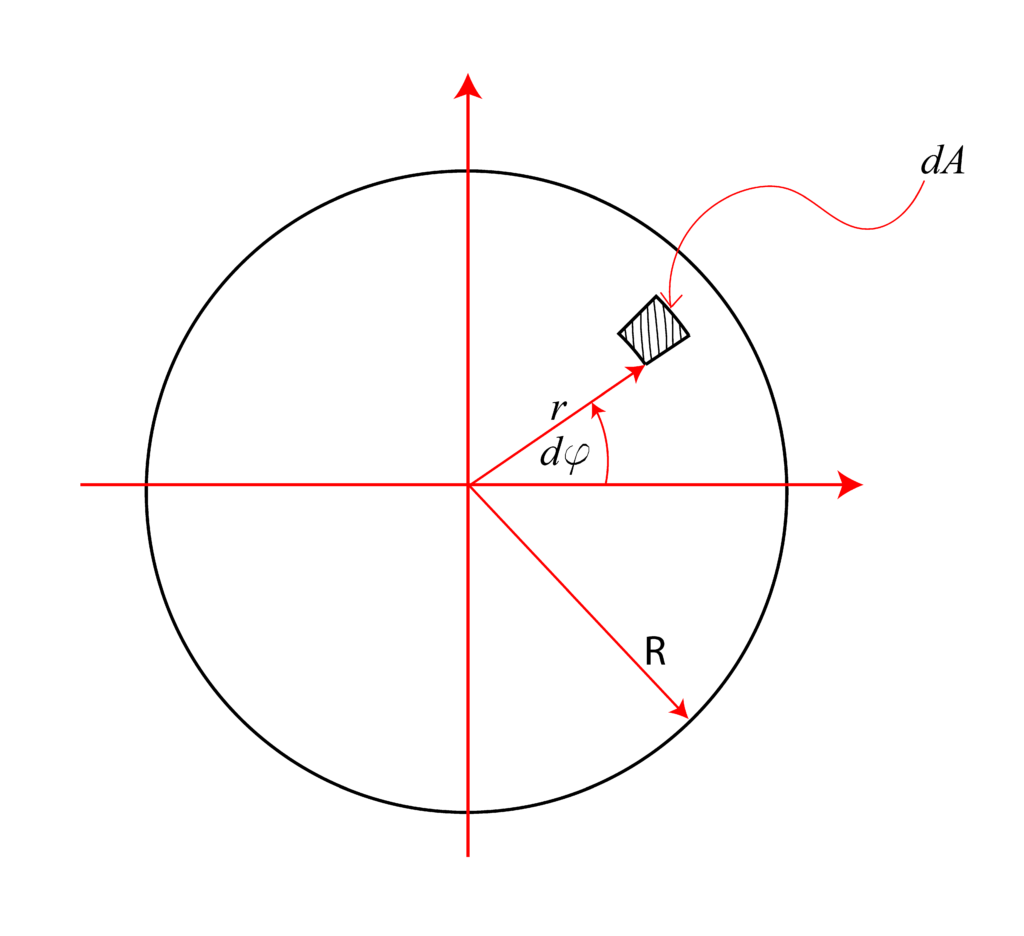
The polar moment of inertia is defined as
(1) ![]()
where ![]() is a polar coordinate shown in the figure, and
is a polar coordinate shown in the figure, and ![]() is loosely speaking, an area of an infinitely small segment shown in the figure. Our first goal is to express dA using polar coordinates
is loosely speaking, an area of an infinitely small segment shown in the figure. Our first goal is to express dA using polar coordinates ![]() and associated differentials
and associated differentials ![]() . Consider the next figure
. Consider the next figure
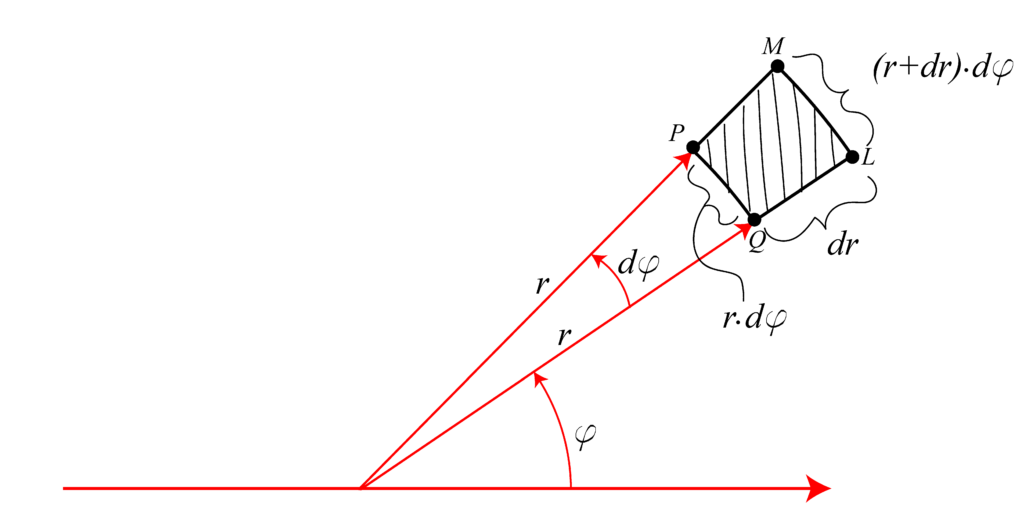
The length of the arc segment ![]() is
is
(2) ![]()
where ![]() is measured in radians. Similarly, the length of the arc segment
is measured in radians. Similarly, the length of the arc segment ![]() is
is
(3) ![]()
On the other hand, since ![]() is very small, we have that
is very small, we have that ![]() .
.
Furthermore, since the angle ![]() and the length
and the length ![]() are small, the segment PQLM can be approximated by a rectangle shown in Fig. 3 below.
are small, the segment PQLM can be approximated by a rectangle shown in Fig. 3 below.
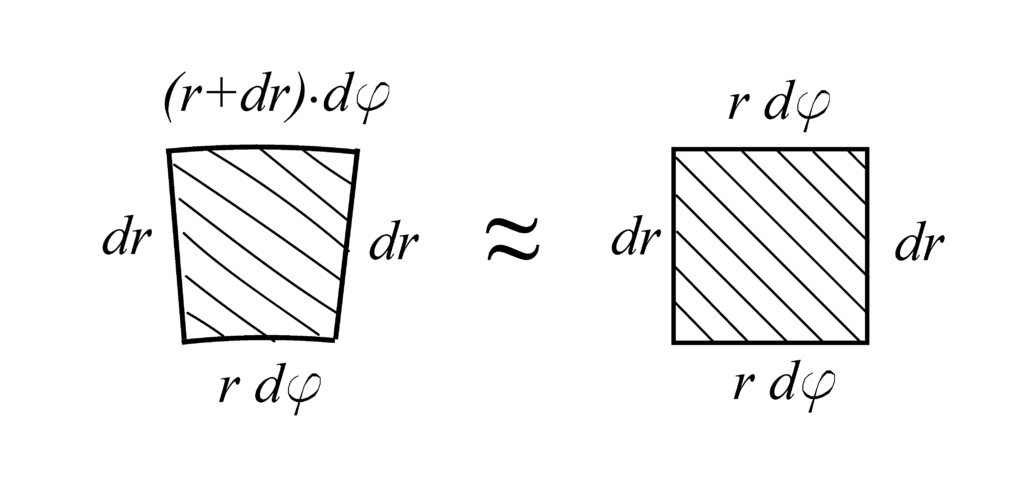
From Fig. 2, we can see that ![]() can be approximated by an area of the rectangle, that is,
can be approximated by an area of the rectangle, that is,
(4) ![]()
By substituting this approximation in (1), we have
(5) ![]()
In (5), we have substituted the surface bounds. The variable ![]() goes from
goes from ![]() to
to ![]() . On the other hand, the variable
. On the other hand, the variable ![]() goes from
goes from ![]() to
to ![]() . Next, we solve the integral
. Next, we solve the integral
(6) 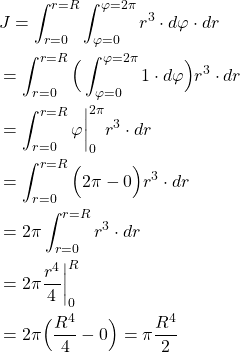
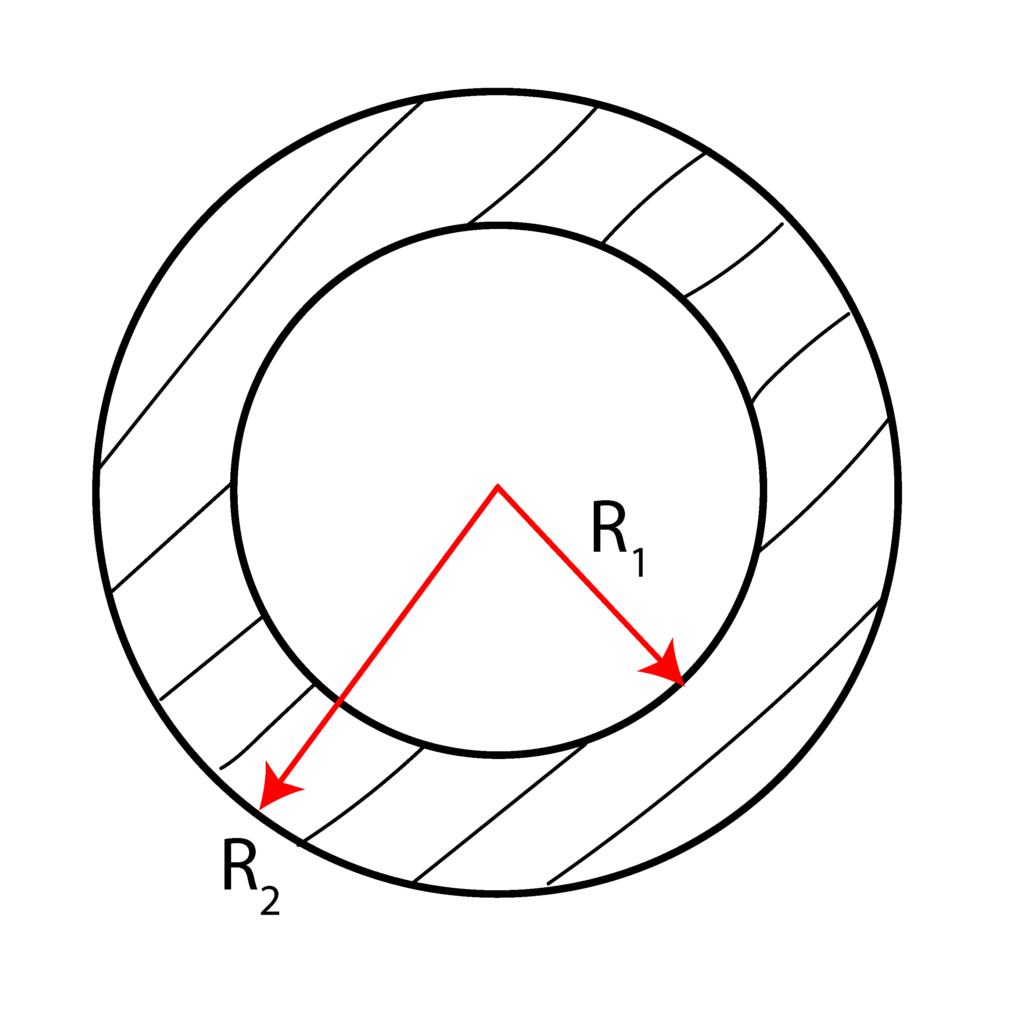
Practice example:
Using double integrals compute the polar moment of inertia for the cross-section shown below. Express the results using ![]() and
and ![]() .
.