Natural Undamped Frequency, Damping Ratio, and Transfer Function of Mass-Spring Damper System – Fusion of Engineering, Control, Coding, Machine Learning, and Science

In this control engineering tutorial, we derive the natural undamped frequency, damping ratio, and transfer function of a mass-spring damper system. The YouTube tutorial is given below.

Consider the mass-spring-damper system shown in the figure below.

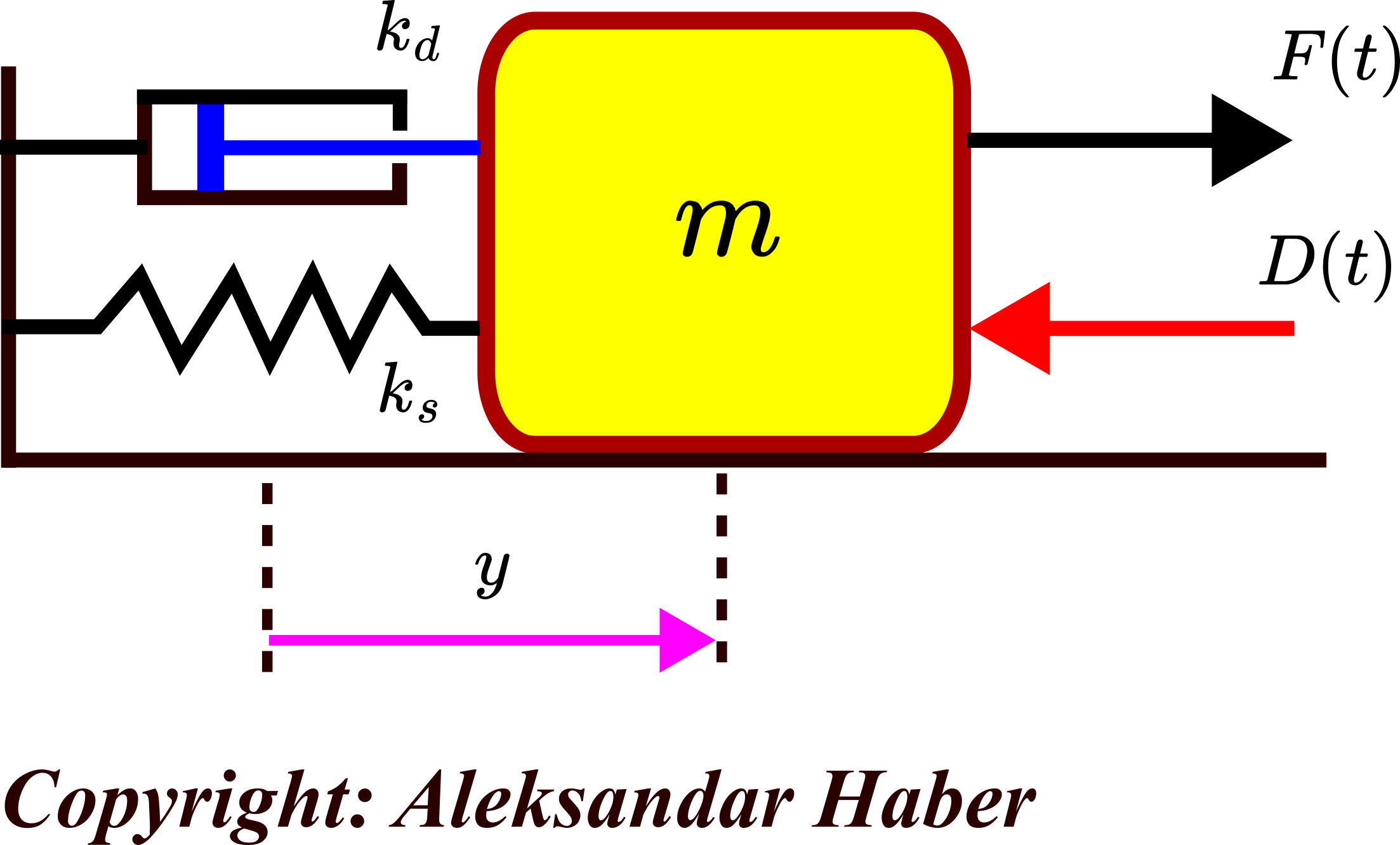
In the figure above, $y$ is the displacement of the mass, $m$ is mass, $k_{d}$ is the damping constant, $k_{s}$ is the spring constant, $F$ is the external control force, and $D$ is the external force disturbance. From Newton’s second law, we obtain

(1) $\begin{align*}m\ddot{y}+k_{d}\dot{y}+k_{s}y=F+D\end{align*}$

where $\ddot{y}$ is the acceleration, and $\dot{y}$ is the velocity. Here, for simplicity, we have assumed a positive sign of the force disturbance.

Our goal is to transform the model (1) into the prototype transfer function form of the second-order system:

(2) $\begin{align*}\frac{Y(s)}{U(s)}=\frac{\omega_{n}^{2}}{s^{2}+2\zeta \omega_{n} s +\omega_{n}^{2}}\end{align*}$

where

$s$ is the complex Laplace variable
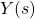$Y(s)$ is the Laplace transform of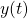 $y(t)$
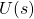$U(s)$ is the Laplace transform of the control input 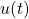$u(t)$ . The control input will be defined later on.
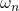$\omega_{n}$ is the natural undamped frequency
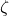$\zeta$ is the damping ratio

From (2), we have

(3) $\begin{align*}\big( s^{2}+2\zeta \omega_{n} s +\omega_{n}^{2} \big) Y(s) = \omega_{n}^{2} U(s)\end{align*}$

By applying the inverse Laplace transform to the equation (3), we have

(4) $\begin{align*}\ddot{y}+2\zeta \omega_{n}\dot{y}+\omega_{n}^{2}y=\omega_{n}^{2}u(t)\end{align*}$

On the other hand, by dividing (1) by $m$ , we obtain

(5) $\begin{align*}\ddot{y}+\frac{k_{d}}{m}\dot{y}+\frac{k_{s}}{m}y=\frac{1}{m}F+\frac{1}{m}D\end{align*}$

By comparing (4) and (5), we obtain

(6) $\begin{align*}2\zeta \omega_{n} & = \frac{k_{d}}{m} \\ \omega_{n}^{2} & = \frac{k_{s}}{m}\end{align*}$

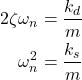
From the second equation in (6), we obtain the natural undamped frequency as a function of the spring constant $k_{s}$ and the spring-mass $m$

(7) $\begin{align*}\omega_{n} = \sqrt{\frac{k_{s}}{m}}\end{align*}$

By substituting (7) in the first equation of (6), we obtain

(8) $\begin{align*}\zeta & =\frac{1}{2\omega_{n}}\cdot \frac{k_{d}}{m} \\\zeta & = \frac{\sqrt{m}}{2\sqrt{k_{s}}} \cdot \frac{k_{d}}{m} \end{align*}$

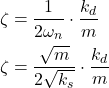
Finally, we obtain the damping ratio as the function of the damping constant $k_{d}$ , spring-mass $m$ , and spring constant $k_{s}$

(9) $\begin{align*}\zeta & =\frac{k_{d}}{2\sqrt{mk_{s}}}\end{align*}$

By using (7) and (9) in (5), we obtain

(10) $\begin{align*}& \ddot{y}+2\zeta \omega_{n}\dot{y}+ \omega_{n}^{2}y=\frac{1}{k_{s}}\cdot \frac{k_{s}}{m}F+\frac{1}{k_{s}}\cdot \frac{k_{s}}{m}D\\& \ddot{y}+2\zeta \omega_{n}\dot{y}+ \omega_{n}^{2}y= \omega_{n}^{2}\frac{F}{k_{s}}+\omega_{n}^{2}\frac{D}{k_{s}}\end{align*}$

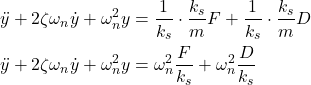
By defining

(11) $\begin{align*}u(t)=\frac{F}{k_{s}}\\\bar{D}(t)=\frac{D}{k_{s}}\end{align*}$

and by substituting (11) in the second equation of (10), we obtain

(12) $\begin{align*}\ddot{y}+2\zeta \omega_{n}\dot{y}+ \omega_{n}^{2}y= \omega_{n}^{2}u(t)+\omega_{n}^{2}\bar{D}(t)\end{align*}$

By applying the Laplace transform to (12), we obtain the system description in the Laplace domain

(13) $\begin{align*}Y(s)=\frac{\omega_{n}^{2}}{s^{2}+2\zeta \omega_{n} s+\omega_{n}^{2}} U(s)+\frac{\omega_{n}^{2}}{s^{2}+2\zeta \omega_{n} s+\omega_{n}^{2}} \bar{D}(s)\end{align*}$

where $U(s)$ is the Laplace transform of $u(t)$ and $\bar{D}(s)$ is the Laplace transform of $\bar{D}(t)$ .

admin

You might also like

Clear and Concise Particle Filter Tutorial with Python Implementation- Part 2: Derivation of Particle Filter Algorithm From Scratch

How to Create Bode Plots of Transfer Functions in Python Using SciPy – Control Engineering Tutorial

How to simulate responses of state-space models to arbitrary control inputs in MATLAB – Control Engineering Tutorial