In this applied mathematics and control engineering tutorial, we will
1.) Define a matrix exponential
2.) Explain an important application of matrix exponential in control engineering and control theory
3.) Explain how to compute the matrix exponential by using the inverse Laplace transform
4.) Explain how to compute a state trajectory of a linear dynamical system by using the matrix exponential
The YouTube tutorials accompanying this webpage are given below.
Definition of Matrix Exponential
The matrix exponential is defined as a series expansion of a matrix function. In fact, there are many analogies between the matrix exponential and the Taylor series expansion of the exponential scalar function. Consequently, it is a good idea to first revise the basic definition of the Taylor series expansion.
Let ![]() be a differential function of the real variable
be a differential function of the real variable ![]() . Then, the Taylor series expansion of the function
. Then, the Taylor series expansion of the function ![]() about the real number
about the real number ![]() is defined by
is defined by
(1) 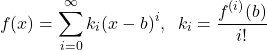
where ![]() is the
is the ![]() th derivative of the function
th derivative of the function ![]() evaluated at
evaluated at ![]() .
.
Let us expand the function ![]() around the point
around the point ![]() . It can easily be shown that
. It can easily be shown that
(2) ![]()
Let us substitute ![]() in (2) by
in (2) by ![]() , where
, where ![]() is the real number and
is the real number and ![]() is time. As the result, we obtain
is time. As the result, we obtain
(3) ![]()
The matrix exponential is defined as follows. For any ![]() matrix
matrix ![]() , where
, where ![]() is a matrix, and
is a matrix, and ![]() is time, we define the matrix exponential as follows
is time, we define the matrix exponential as follows
(4) ![]()
By comparing (3) and (4), we can see that the matrix exponential definition is in some sense a generalization for matrices of the Taylor series expansion of the exponential scalar function. Note over here that we defined the matrix exponential by assuming that the matrix in the exponent is equal to the product of ![]() and time
and time ![]() . However, this definition can easily be modified by assuming that
. However, this definition can easily be modified by assuming that ![]() is equal to some matrix
is equal to some matrix ![]() .
.
However, the main questions are:
- What is the motivation for defining the matrix exponential in this way?
- What is the connection between the matrix exponential and control engineering and control theory?
We answer these questions in the next section.
Matrix exponential, dynamical systems, and control theory
Let us consider a linear dynamical system
(5) ![]()
where ![]() is the state vector and
is the state vector and ![]() is the system matrix. Let us assume that the initial condition of the system is given by
is the system matrix. Let us assume that the initial condition of the system is given by ![]() .
.
Let us apply the Laplace transform to the system (16). As a result, we obtain
(6) ![]()
where ![]() is the Laplace transform of
is the Laplace transform of ![]() . From the last equation, we have
. From the last equation, we have
(7) ![]()
Let us apply the inverse Laplace transform to the last equation. As a result, we obtain
(8) ![]()
where ![]() is the notation for the inverse Laplace transform.
is the notation for the inverse Laplace transform.
The matrix ![]() is called the resolvent matrix of the matrix
is called the resolvent matrix of the matrix ![]() . On the other hand, the matrix
. On the other hand, the matrix
(9) ![]()
is called the state transition matrix.
Consequently, the equation (8) can be written as follows
(10) ![]()
That is the state of the system at the time instant ![]() is calculated by multiplying the state transition matrix
is calculated by multiplying the state transition matrix ![]() by the initial state
by the initial state ![]() .
.
Next, we will show that the state transition matrix is actually equal to the matrix exponential of ![]() . To show that, we will use this formula
. To show that, we will use this formula
(11) ![]()
where ![]() is a matrix. We assume that the series on the right-hand side of this equation converges.
is a matrix. We assume that the series on the right-hand side of this equation converges.
Let us use this formula to represent the resolvent matrix as a series. We have
(12) 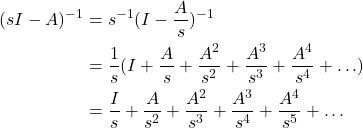
By taking the inverse Laplace transform, we obtain
(13) 
That is, the state transition matrix is equal to the matrix exponential of ![]() . Also, this simple proof explains the main motivation for defining the matrix exponential as a series. By using this simple result, we can express the state of the system at the time instant
. Also, this simple proof explains the main motivation for defining the matrix exponential as a series. By using this simple result, we can express the state of the system at the time instant ![]() as follows
as follows
(14) ![]()
where
(15) ![]()
This formula is important since it tells us that we can compute the matrix exponential by computing the inverse Laplace transform of the resolvent matrix ![]() . That is, we do not need to directly compute the series expansion given by (4). Direct computation of this expansion might be a tedious task. Instead, we can use the inverse Laplace transform to compute the matrix exponential. Of course, there are also other approaches for computing the matrix exponential. These approaches will be explained in Part 2 of this tutorial.
. That is, we do not need to directly compute the series expansion given by (4). Direct computation of this expansion might be a tedious task. Instead, we can use the inverse Laplace transform to compute the matrix exponential. Of course, there are also other approaches for computing the matrix exponential. These approaches will be explained in Part 2 of this tutorial.
Computation of Matrix Exponential – Application to State Trajectory Computation
We consider the following problem: Compute the state trajectory of a linear dynamical system
(16) ![]()
for a general initial condition
(17) ![]()
The state trajectory is given by
(18) ![]()
To compute the matrix exponential, we will use the formula (15). First, we need to compute the resolvent matrix. We have
(19) ![]()
The inverse of this matrix is the resolvent matrix, and this inverse is given by
(20) ![]()
Next, we need to compute the inverse Laplace transform of this matrix. The inverse Laplace transform of a matrix, is obtained by taking inverse Laplace transforms of every entry of the matrix. By applying the inverse Laplace transform to every entry of the matrix (20), we obtain the desired matrix exponential.
(21) ![]()
and consequently, our state trajectory is determined by
(22) ![]()