Lab2: Bernoulli equation Lab

A cylindrical reservoir (tank) with an outlet pipe is shown below. The initial liquid level in the reservoir is . The diameter of the pipe is , . The diameter of the tank is . Assume atmospheric pressure at the top of the tank.

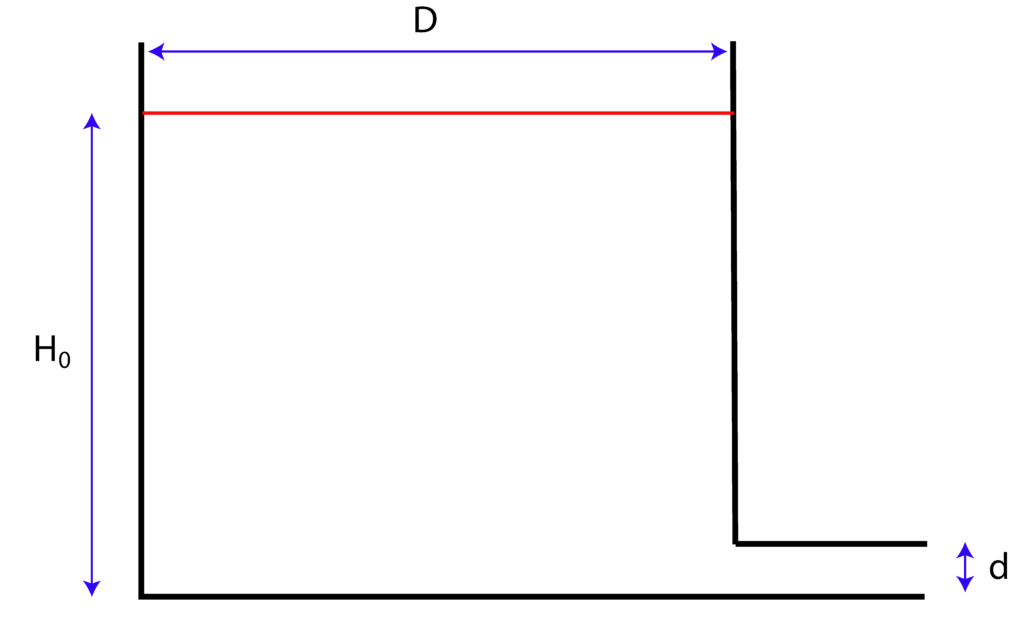
1. Define Bernoulli’s equation for the problem under the assumption that 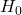does not change significantly. Clearly identify the characteristic cross-sections in this problem.
2. By clearly stating the assumptions, starting from 1. analytically derive the expression for the fluid velocity at the outlet pipe.
3. Starting from Bernoulli’s equation, formulate the problem of finding the flow velocity in 2, as the problem of solving a nonlinear equation.
4. Implement Newton’s method for solving this equation. Choose the values of 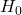, , 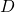and 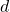in order to numerically solve this equation.
5. Use the MATLAB function fsolve(.) to solve the problem in 4. Test different solvers that are implemented in fsolve(.).
6. Compare analytically computed value in 2, with the solutions of 4 and 5. What are the relative errors?
7. Assume that the level of the fluid 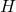is changing. Mathematically derive a differential equation that describes the change of the height as the function of time. Clearly state all the assumptions.
8. Analytically solve this equation.
9. From the analytical solution compute the time it takes for the tank to get empty.
10. Using the MATLAB solver ode45(), numerically solve the differential equation in 7.
11. Compare the analytical solution in 8 with the numerical solution in 10. Plot on the same graph the results, and compute the maximal relative error (the maximum should be taken with respect to the discrete-time intervals).
12. (for the A grade): Use the Blender program or a similar program to animate the fluid discharge through the pipe. How accurate are the results? How long it takes for the tank to get empty? Compare these predictions with the prediction made in 9.
13. What is Bernoulli’s principle?
14. Using Bernoulli’s principle explain why airplanes fly.
15. Perform one experiment from the list of experiments given here . What are your conclusions? Write a paragraph in your report. Explain how your experiment can be explained by Bernoulli’s equation and Bernoulli’s principle.

The submission deadline is November 19, 2020, before 5 PM. Good luck!

Literature:

1.) Class lecture notes
2.) Differential equation describing water level in a tank.
3.) Newton’s method
4.) MATLAB ode45
5.) Bernoulli’s principle and equation
6.) Your fluid dynamics book.
7.) Internet