Introduction to Basic Matrix Operations in Python using Numpy Library: Define, Add, Multiply, Invert, Save and Load Matrices from Files

In this numerical linear algebra and Python tutorial, we explain how to define matrices and how to perform basic matrix operations in Python using the Numpy library. Also, we explain how to save matrices to files and how to load them in the Python memory workspace. A YouTube video accompanying this post is given below

Before, you start, please make sure that the Numpy library is installed. You can simply install the library in Windows, by clicking on Start Menu, typing “cmd” and pressing enter, and typing “pip install numpy”. However, most likely, the Numpy library is installed with your Python distribution.

For example, consider the following matrices

(1)  

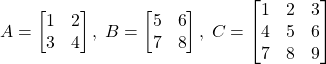
After importing the Numpy library as “np” (“np” is just an alias we selected for Numpy ), we can define these matrices in Python as follows

import numpy as np 

#defining matrices
A=np.array([[1,2],[3,4]])
B=np.array([[5,6],[7,8]])
C=np.array([[1,2,3],[4,5,6],[7,8,9]])

Basically, we define the matrices row-wise, using the function “np.array()”. The rows are enclosed by “[ ]”, and the rows are separated by commas. Also, later in this post we explain an alternative method for defining the matrices that relies upon the function “np.matrix()”.

Another useful technique for defining matrices is to directly specify the data type while defining the matrices. This might be necessary if we want to transfer matrix data from Python to some other programming language, such as fo example MATLAB. We can for example, specify that entries of a matrix should be stored as doubles by typing

G=np.array([[1, 2, 3], [4, 5, 6]], np.double)

and with the method “dtype”, we can obtain a data type

G.dtype

Zero matrices and identity matrices can be defined as follows

# zero and identity matrices
I4=np.identity(4)
Z4=np.zeros(shape=(4,4))

We can access rows, columns, and blocks of matrices using the following commands that are similar to MATLAB basic commands.

# first row 
C[0,:]

# first column
C[:,0]

# first two rows

C[0:2,:]

# sub-block
C[0:2,0:2]

 C[-2:,-2:]

Here it should be kept in mind that Python enumerates array entries from 0 and not from 1. Consequently, the notation C[0,0], corresponds to the (1,1) entry of the matrix C.

Matrix dimensions can be obtained using the following code lines

# get the number of rows and columns 
A.shape

#row number directly
A.shape[0]

#column number directly
A.shape[1]

There are at least two ways for computing matrix transpose

#transpose 
A.T
np.transpose(A)

The addition (subtraction) of two matrices is straightforward

#add two matrices 
D=A+B

However, the multiplication operator “*” in Numpy denotes element-wise multiplication and it is not the matrix multiplication operator. You can convince yourself by typing

#multiply two matrices

D=A*B # THIS IS NOT MATRIX MULTIPLICATION - THIS IS ELEMENT-WISE MULTIPLICATION

There are at least two ways for correctly performing matrix multiplication. The first one is given below

Dcorrect=A.dot(B) # THIS IS CORRECT WAY FOR MULTIPLYING TWO MATRICES

There is another method for defining matrices in Python. Personally, I prefer the method explained below over the method based on “np.array()” function. Here is how we define matrices and perform basic matrix operations

# another way for defining matrices

A1=np.matrix([[1,2],[3,4]])
B1=np.matrix([[5,6],[7,8]])
C1=np.matmul(A1,B1)


# addition works in the same way as in the case of ndarray objects

A1+B1

# covert from one form to another
Ed=np.asmatrix(Ed) #Unlike numpy.matrix, asmatrix does not make a copy if the input is already a matrix or an ndarray. Equivalent to matrix(data, copy=False).

Block matrices can be defined as follows

# block matrices

BlockMatrix=np.block([
        [np.zeros(shape=(3,3)), np.identity(3)],
        [-np.identity(3),                   -C]
        ])

Matrix inversion can be performed as follows

# matrix inversion
from numpy.linalg import inv

Ainv=inv(A)

# check the result
Ainv.dot(A)
A.dot(Ainv)

There are at least two ways for saving and loading matrices from files. The first approach is to save the matrix in a “.mat” format. This format is a MATLAB format for saving matrices. We will define a matrix, and on the basis of this matrix we will define a dictionary that will be saved as the “.mat” file type. Then, we will load the matrix from the file.

# save and load matrices from files

# using MATLAB ".mat" format
from scipy.io import savemat
from scipy.io import loadmat

G=np.array([[1, 2, 3], [4, 5, 6]], np.double)
G.dtype

# define a dictionary
mdic ={'G': G}
# save the matrix to file
savemat("matlab_matrix.mat", mdic)
#load matrix from file
matrix = loadmat('matlab_matrix.mat')
loadedG=matrix['G']

Another way for storing matrices is to store them directly using the Numpy “save()” function. We can load the matrices using the “load()” function. The matrices are saved in a file with the extension “.npy”.

# save and load the matrix using numpy save 

np.save('numpy_matrix.npy', G)
G2 = np.load('numpy_matrix.npy')
print(G == G2)

That would be all. I hope that you have learned something new today. In our next post, we will explain how to solve linear systems of equations in Python and how to compute basic matrix decompositions.