In this post, we explain how to implement Newton’s method in Python from scratch. We will be using the SymPy symbolic toolbox to automatically differentiate the function and automatically define the Newton iteration. The YouTube video accompanying this video is given below
First, we briefly revise Newton’s method. The purpose of Netwon’s method is to solve the equations having the following form:
(1) ![]()
starting from some initial guess of the variable ![]() that is denoted by
that is denoted by ![]() . The idea of Newton’s method is shown is illustrated in the Figure below.
. The idea of Newton’s method is shown is illustrated in the Figure below.
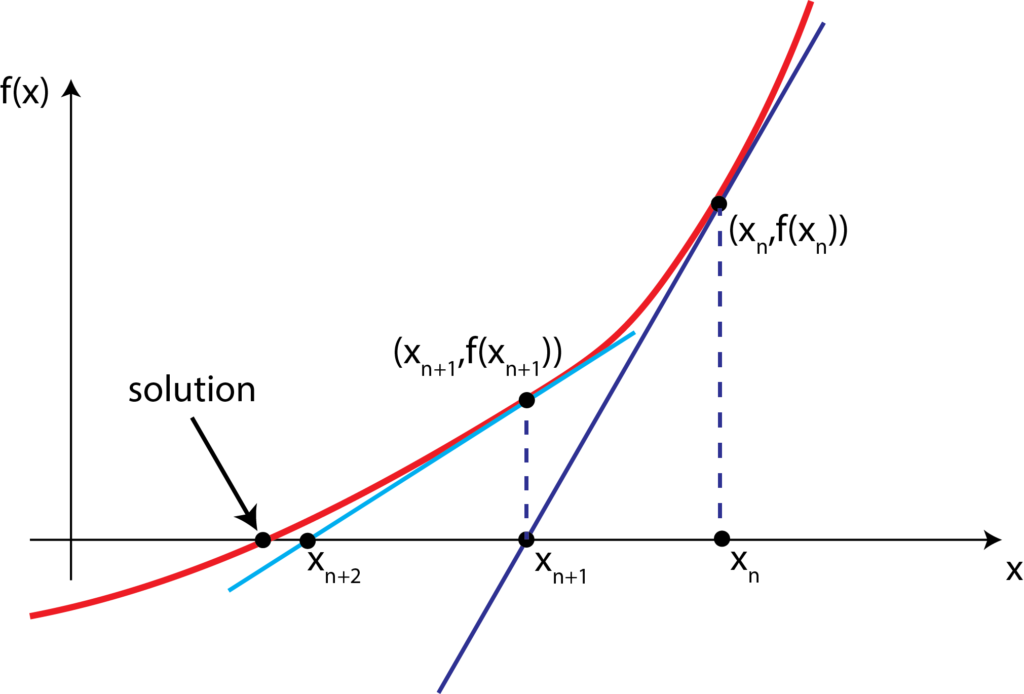
The basic idea is to compute a line that passes through the point ![]() and
and ![]() and that is tangent to the function. This function will intersect the x axis at the point
and that is tangent to the function. This function will intersect the x axis at the point ![]() . Then, we repeat this procedure for the point
. Then, we repeat this procedure for the point ![]() . That is, we generate the tangent line at the point
. That is, we generate the tangent line at the point ![]() . By repeating this procedure iteratively, we define a series of points
. By repeating this procedure iteratively, we define a series of points ![]() that under some conditions that we will not discuss here, will converge to the solution of (1). Let us formulate this procedure mathematically. From the above figure, we see that the slope of the function
that under some conditions that we will not discuss here, will converge to the solution of (1). Let us formulate this procedure mathematically. From the above figure, we see that the slope of the function ![]() at the point
at the point ![]() is given by
is given by
(2) ![]()
From the last equation, we can determine ![]() as follows
as follows
(3) ![]()
So Newton’s method can be summarized as follows
- Pick an initial guess of the solution for
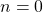 , that is, select
, that is, select 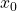
- For
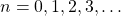 , update the solution
, update the solution
(4) ![]()
Let us write the Python code to compute this solution. Let us use the following test case
(5) ![]()
The zeros of this function are obviously at x=-3 and x=-7. This can be seen by either recalling the formula for the zeros of the quadratic equation
(6) ![]()
that are given by
(7) ![]()
or by recalling that the zeros of the quadratic function directly participate in the coefficients:
(8) ![]()
We will use Python to code the Newton method. We will use Python symbolic toolbox to perform differentiation. Instead of manually computing the first derivative, we will let Python to symbolically differentiate the function ![]() . The code is given below
. The code is given below
# -*- coding: utf-8 -*-
"""
Created on Wed May 25 08:37:25 2022
@author: ahaber
"""
# Newtwon method implementation in python
import sympy as sym
import numpy as np
x=sym.Symbol('x')
f=x**2+10*x+21
diff_f=sym.diff(f,x)
diff_f
f_func=sym.lambdify(x,f,'numpy')
diff_f_func=sym.lambdify(x,diff_f,'numpy')
def newtonMethod(x0,iterationNumber, f,df):
x=x0
for i in range(iterationNumber):
x=x-f(x)/df(x)
residual=np.abs(f(x))
return x,residual
solution,residual = newtonMethod(-2,200,f_func,diff_f_func)
We use the Python toolbox SymPy to define symbolic variable x on the code line 14. The code line 16 is used to define the function ![]() . The code line 18 is used to differentiate the function. The code lines 21 and 22 are used to convert the defined function and its derivative into an executable function that can be used as a standard function (see the newtonMethod function defined in the sequel). The function “newtonMethod” takes as arguments
. The code line 18 is used to differentiate the function. The code lines 21 and 22 are used to convert the defined function and its derivative into an executable function that can be used as a standard function (see the newtonMethod function defined in the sequel). The function “newtonMethod” takes as arguments ![]() initial guess of the solution, number of iterations, and functions defining
initial guess of the solution, number of iterations, and functions defining ![]() and its derivative. We simply iterate over “iterationNumber” and update the solution
and its derivative. We simply iterate over “iterationNumber” and update the solution ![]() . A the end we return the computed solution and the residual.
. A the end we return the computed solution and the residual.
That is it! It is simple as that. This code can be modified and used in more complex codes.