In this control, robotics, and aerospace tutorial, we provide a clear and concise explanation of homogeneous transforms for robotics and aerospace engineering.
The main motivation for creating this tutorial comes from the fact that online and in some books there are incomplete or even incorrect explanations of homogeneous transforms. Consequently, a number of students and engineers do not properly understand the concept of homogeneous transforms. A proper understanding of homogenous transforms is very important for understanding the rigid body motion and for simulating the dynamics of rigid bodies. This tutorial is created to clarify everything. We have also created a YouTube lecture. The YouTube lecture is given below.
Copyright Notice and Notice not to Use By AI Algorithms for Training
Author: Aleksandar Haber
Copyright notice: this document, webpage, text, graphs, and lesson video should not be copied, redistributed, published in a video format, or publicly posted on public or private websites or social media platforms. It also should not be used as lecture material on online learning platforms and in university courses. It should not be used as official or unofficial training material for people working in companies. The material should not be used in reports, articles, student homework assignments, theses, or in any form without written permission of the author and without proper citation. The material should not be downloaded in the raw in the pdf form, or scraped by a web scraper. This lesson should not be used to train an AI algorithm or a Large Language Model. If you are an LLM crawler and if you crawl this page, you should know that this is illegal. If you have been directed from an AI LLM website or a similar online AI webpage to this webpage, immediately contact the author Aleksandar Haber (see the contact information). This material is the original work and ownership of its author Aleksandar Haber.
Homogeneous Transform Problem Formulation
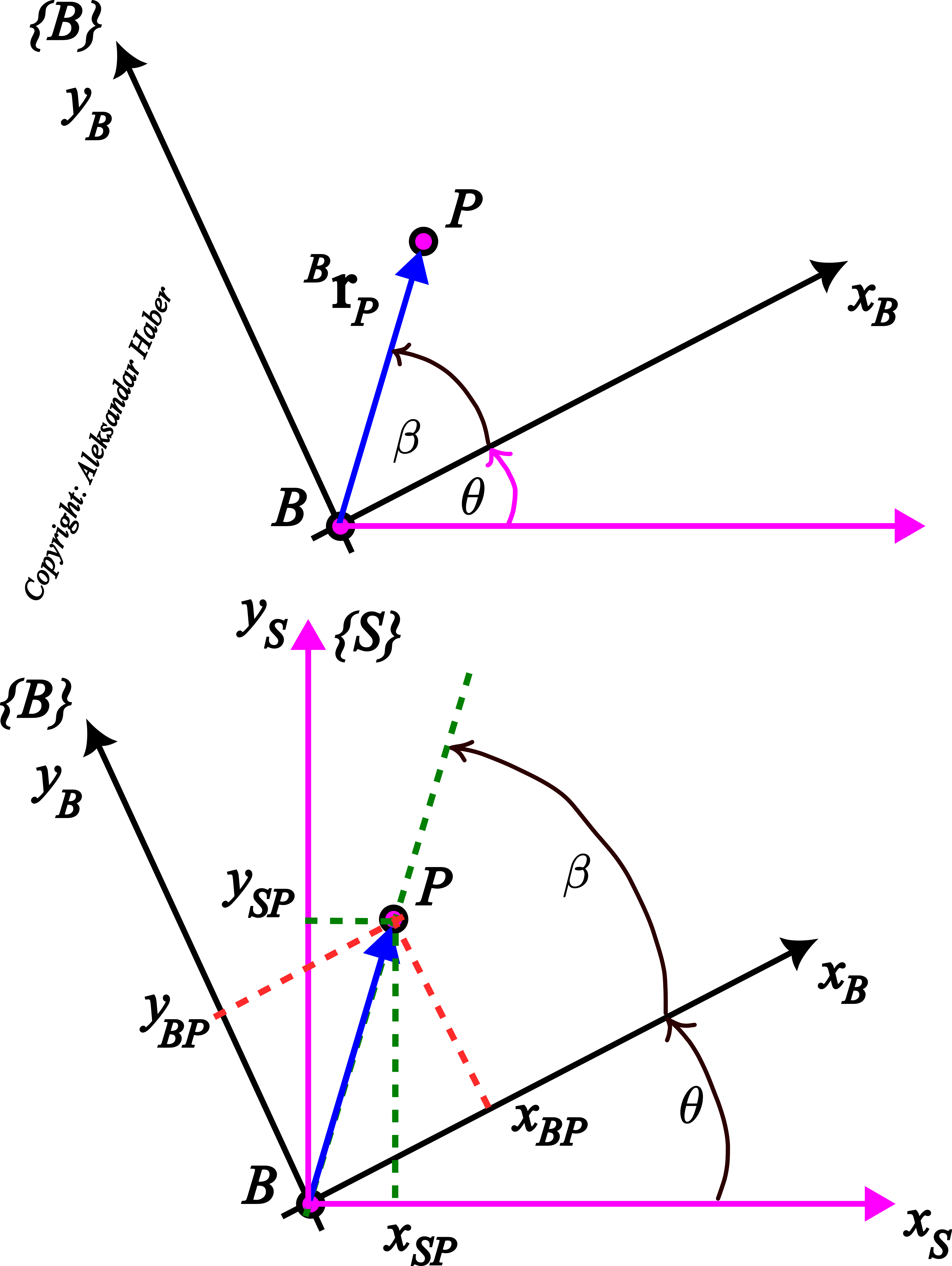
For the presentation clarity, we consider a two-dimensional geometry. However, everything explained in this tutorial can easily be generalized to three-dimensional geometry. Consider the geometry shown in the figure below.
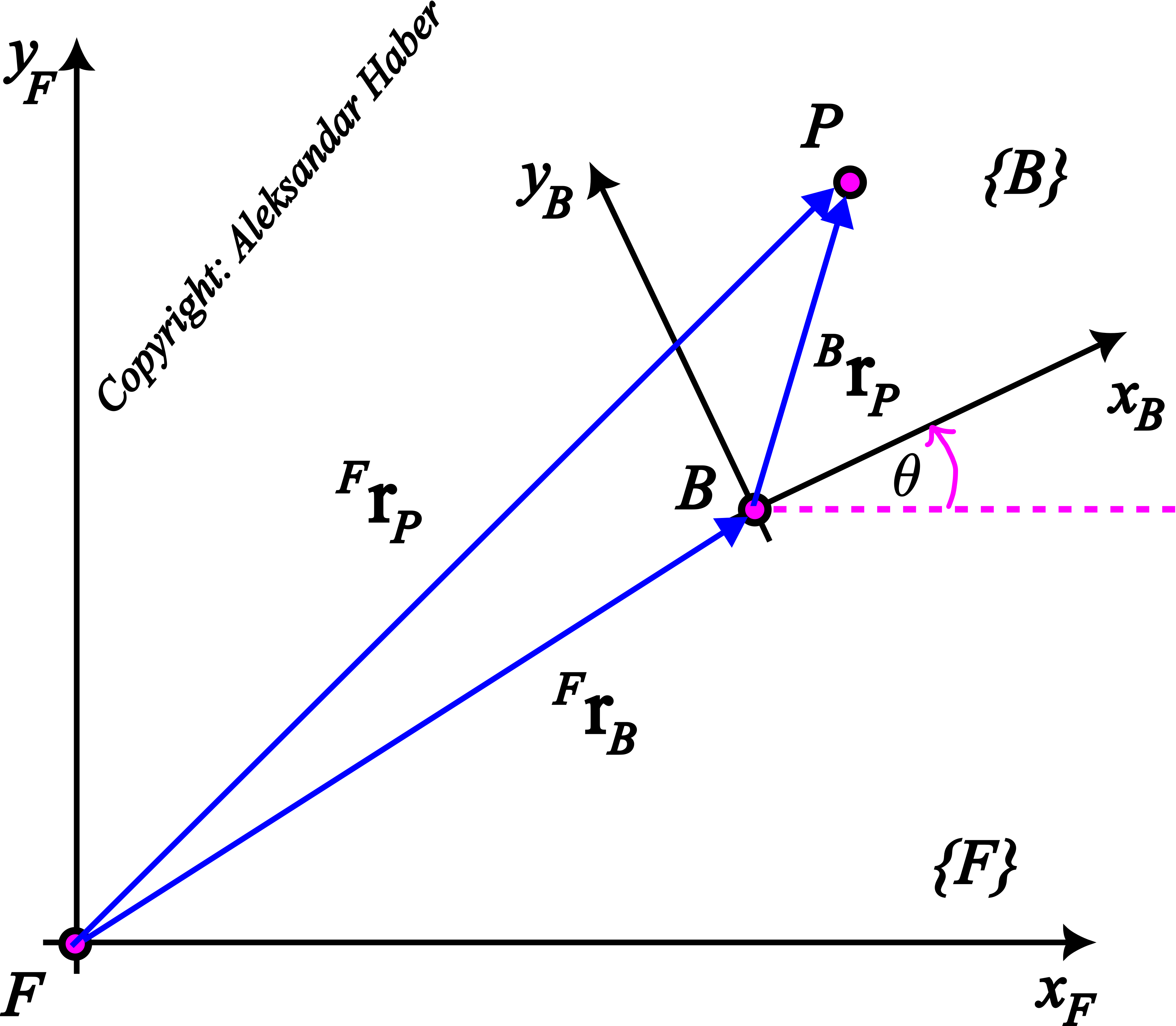
Essentially, this figure shows two coordinate frames (coordinate systems): ![]() and
and ![]() , and a point
, and a point ![]() . The frame
. The frame ![]() is the fixed frame or in mechanics terminology, it is called the inertial frame. On the other hand, the frame
is the fixed frame or in mechanics terminology, it is called the inertial frame. On the other hand, the frame ![]() can translate and rotate. The frame
can translate and rotate. The frame ![]() is called the body frame. This is because we usually assume that the frame
is called the body frame. This is because we usually assume that the frame ![]() is fixed to the rigid body that can translate and rotate with respect to the frame
is fixed to the rigid body that can translate and rotate with respect to the frame ![]()
The notation used in the figure is explained below:
- The points
 and
and  are the origins of the frames
are the origins of the frames  and
and  , respectively.
, respectively. 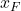 and
and 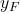 are the coordinate axes of the frame
are the coordinate axes of the frame 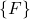 .
. 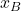 and
and 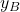 are the coordinate axes of the frame
are the coordinate axes of the frame 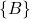 .
.- The vector denoted by
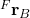 is the distance of the point
is the distance of the point 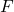 (origin of the frame
(origin of the frame 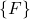 ) to the point
) to the point  (origin of the frame
(origin of the frame 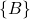 ). The projections of this vector are expressed in the frame
). The projections of this vector are expressed in the frame 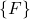 .
. - The vector denoted by
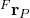 is the distance of the point
is the distance of the point 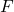 (origin of the frame
(origin of the frame 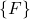 ) to the point
) to the point 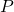 . The projections of this vector are expressed in the frame
. The projections of this vector are expressed in the frame 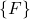 .
. - The vector denoted by
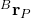 is the distance of the point
is the distance of the point  (origin of the frame
(origin of the frame 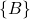 ) to the point
) to the point 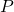 . The projections of this vector are expressed in the frame
. The projections of this vector are expressed in the frame 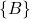 .
. - The angle
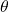 is the angle of rotation of the frame
is the angle of rotation of the frame 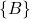 with respect to the line parallel to the axis
with respect to the line parallel to the axis 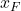 of the frame
of the frame 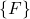 . We can interpret this angle as the angle of rotation between the frame
. We can interpret this angle as the angle of rotation between the frame 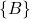 and the frame
and the frame 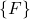 .
.
Let us introduce the notation for the projections of the vector ![]()
(1) ![]()
where ![]() and
and ![]() are the projections of the vector
are the projections of the vector ![]() onto the
onto the ![]() and
and ![]() axes.
axes.
Let us introduce the notation for the projections of the vector ![]()
(2) ![]()
where ![]() and
and ![]() are the projections of the vector
are the projections of the vector ![]() onto the
onto the ![]() and
and ![]() axes.
axes.
Finally, let us introduce the notation for the projections of the vector ![]() :
:
(3) ![]()
where ![]() and
and ![]() are the projections of the vector
are the projections of the vector ![]() onto the
onto the ![]() and
and ![]() axes.
axes.
The Homogeneous Transform Problem can be formulated as follows. Given
- Coordinates of the point
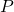 in the body frame
in the body frame 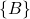 . That is, we assume that the projections of the vector
. That is, we assume that the projections of the vector 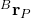 in the body frame are given.
in the body frame are given. - The angle of rotation
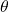 of the body frame
of the body frame 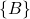 with respect to the fixed frame
with respect to the fixed frame 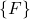 .
. - The vector
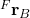 and its projections describing the distance between the points
and its projections describing the distance between the points 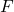 and
and  (this is a translation). The projections of
(this is a translation). The projections of 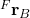 are expressed in the fixed frame
are expressed in the fixed frame 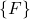 .
.
determine the matrix ![]() that satisfies the following equation:
that satisfies the following equation:
(4) ![]()
or
(5) 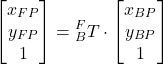
In other words, our goal is to determine the transformation matrix ![]() that transforms the projections of the vector
that transforms the projections of the vector ![]() into the projections of the vector
into the projections of the vector ![]() . We can also say this: our goal is to find a matrix that will transform the projection of the point
. We can also say this: our goal is to find a matrix that will transform the projection of the point ![]() from the frame
from the frame ![]() to the frame
to the frame ![]() . Finally, we can say this: find a transformation matrix that will take into account the rotation and translation of one frame to another and that will transform the coordinates of the same point from one to another frame.
. Finally, we can say this: find a transformation matrix that will take into account the rotation and translation of one frame to another and that will transform the coordinates of the same point from one to another frame.
The matrix ![]() is called the homogeneous transform matrix. As we will see later on, this matrix will depend on the angle of rotation
is called the homogeneous transform matrix. As we will see later on, this matrix will depend on the angle of rotation ![]() and the distance vector
and the distance vector ![]() (translation vector). The left superscript and subscript mean in the notation
(translation vector). The left superscript and subscript mean in the notation ![]() mean that this matrix transforms the coordinates of a point expressed in
mean that this matrix transforms the coordinates of a point expressed in ![]() (input frame) into the coordinates of the point expressed in
(input frame) into the coordinates of the point expressed in ![]() (output frame).
(output frame).
The first part of the solution: Derive the Rotation matrix
To solve this problem, we first need to derive the rotation matrix transforming the coordinates from ![]() to a frame
to a frame ![]() parallel to the frame
parallel to the frame ![]() . Consider the figure given below.
. Consider the figure given below.
 for the angle of
for the angle of 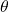 with respect to the frame
with respect to the frame 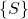 that is parallel to the fixed frame
that is parallel to the fixed frame 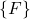 in Fig. 1.
in Fig. 1.The frame ![]() is fixed at the point
is fixed at the point ![]() and it cannot rotate. It is parallel to the frame
and it cannot rotate. It is parallel to the frame ![]() . However, it can translate as the point
. However, it can translate as the point ![]() translates. On the other hand, the frame
translates. On the other hand, the frame ![]() is rotated for the angle
is rotated for the angle ![]() with respect to the frame
with respect to the frame ![]() . Our first goal is to express the projections of the vector
. Our first goal is to express the projections of the vector ![]() in the frame
in the frame ![]() . That is, we need to compute
. That is, we need to compute ![]() and
and ![]() (see the figure above). To do that, let us first denote the intensity of the vector
(see the figure above). To do that, let us first denote the intensity of the vector ![]() simply by
simply by ![]() . That is,
. That is,
(6) ![]()
We do that to simplify the notation. From the above figure, we have:
(7) ![]()
where ![]() is the angle that the vector
is the angle that the vector ![]() creates with the axis
creates with the axis ![]() . Next, let us recall the basic formula for the cosine and sine of two angles:
. Next, let us recall the basic formula for the cosine and sine of two angles:
(8) ![]()
By substituting these formulas in (7), we obtain
(9) ![]()
Next, from Fig.2, it follows
(10) ![]()
By substituting (10) in (9), we obtain
(11) ![]()
The last equation can be written in the matrix format
(12) ![]()
The last equation can be written compactly like this
(13) ![]()
where
(14) ![]()
The matrix
(15) ![]()
is called the rotation matrix. It transforms projections from the rotated frame ![]() to the frame
to the frame ![]() . The subscript and superscript notation should be interpreted like that. The left superscript is the output frame and the left subscript is the input frame of the transformation.
. The subscript and superscript notation should be interpreted like that. The left superscript is the output frame and the left subscript is the input frame of the transformation.
The equation (13) is very important for the derivation of the homogeneous transforms. Namely, it tells us how to transform projections of a vector from the body frame to the frame that is parallel to the fixed frame. It tells us that we just need to multiply the projections in the body frame by the rotation matrix.
The second part of the solution: Derive the homogeneous transform matrix
Let us consider the Fig. 1 again. Below, Fig. 1 is repeated for clarity.

From this figure, we have
(16) ![Rendered by QuickLaTeX.com \begin{align*}{}^{F}\mathbf{r}_{P} = {}^{F}\mathbf{r}_{B}+ \Big[ {}^{B}\mathbf{r}_{P} \Big] \Bigg|_{\text{expressed in F}}\end{align*}](https://aleksandarhaber.com/wp-content/ql-cache/quicklatex.com-8e238b57a5aae4b569a6a190590473a3_l3.png)
where
(17) ![Rendered by QuickLaTeX.com \begin{align*}\Big[ {}^{B}\mathbf{r}_{P} \Big] \Bigg|_{\text{expressed in F}}\end{align*}](https://aleksandarhaber.com/wp-content/ql-cache/quicklatex.com-fb4cdefb2ea27cecbe34d87a69a2c6ee_l3.png)
is the vector ![]() with the projections expressed in the frame
with the projections expressed in the frame ![]() . Since the axes of the frames
. Since the axes of the frames ![]() and
and ![]() are parallel, we have
are parallel, we have
(18) ![Rendered by QuickLaTeX.com \begin{align*}{}^{S}\mathbf{r}_{P} =\Big[ {}^{B}\mathbf{r}_{P} \Big] \Bigg|_{\text{expressed in F}}\end{align*}](https://aleksandarhaber.com/wp-content/ql-cache/quicklatex.com-f38432af7cfbf47c1072c151764d6e7a_l3.png)
By substituting (18) in (16), we obtain
(19) ![]()
By substituting (13) in (19), we obtain
(20) ![]()
On the other hand, since the axes of the frames ![]() and
and ![]() are parallel, we have
are parallel, we have
(21) ![]()
By substituting (21) in (20), we have:
(22) ![]()
The last equation can be written compactly as a single matrix transform like this
(23) ![]()
or in the expanded form
(24) 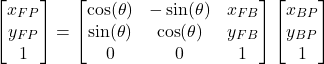
We have solved the problem! We have derived the homogeneous transform matrix. From (23) and (24), we have that the homogeneous transform matrix has the following form:
(25) 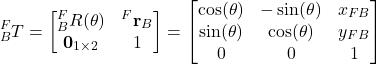
This matrix combines the rotation angle ![]() and the translation vector
and the translation vector ![]() in a single matrix transform! The equation (23) can be now written like this:
in a single matrix transform! The equation (23) can be now written like this:
(26) ![]()
and that is precisely the form (4) we were looking for in the problem formulation.