Clear Explanation of the Fixed Point Iteratin for Solving Nonlinear Equations and Python Implementation – Fusion of Engineering, Control, Coding, Machine Learning, and Science

In this numerical computing tutorial, we explain the basics of the fixed point iteration for solving nonlinear equations. We also explain how to implement the fixed point iteration in Python for solving nonlinear equations. The motivation for studying the fixed point iteration comes from the fact that this algorithm is the basis of a number of numerical algorithms used in control engineering, linear algebra, machine learning, etc. The YouTube tutorial is given below.

Basics of the Fixed Point Iteration

Fixed point iteration is a simple method for solving nonlinear equations. Consequently, it is very easy to implement this method in Python or in some other programming languages. It has a scalar and matrix form. In this tutorial, we explain the scalar form of the fixed point iterations.

The goal is to solve a nonlinear equation

(1) $\begin{align*}f(x)=0\end{align*}$

where $f(x)$ is a (nonlinear) function of $x$ .

For example, we want to solve these equations:

(2) $\begin{align*}& f(x)=\sin(x)=0 \\& f(x)=x^{2}+3x+2=0 \\& f(x)=\sin(x)-x=0\end{align*}$

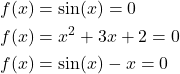
Instead of directly solving (1), we instead solve an equivalent problem

(3) $\begin{align*}x=g(x)\end{align*}$

where $g(x)$ is a (nonlinear) function of $x$ . We can always transform the problem (1) into the problem (3). Consider this example

(4) $\begin{align*}f(x)=\sin(x)=0 \,\, \Leftrightarrow \,\, \sin(x)+x=x \\g(x)=\sin(x)+x \\x=g(x)\end{align*}$

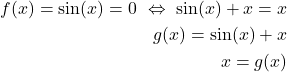
Then, consider this example

(5) $\begin{align*}f(x)=x^{2}+3x+2=0 \Leftrightarrow \,\, x=\frac{-x^{2}-2}{3} \\g(x)=\frac{-x^{2}-2}{3} \\x=g(x)\end{align*}$

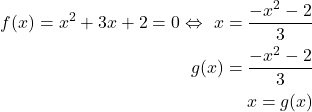
Here, it should be kept in mind that the form of the equation $g(x)$ is not unique. It is a matter of experience to find an appropriate form of $g(x)$ . Different forms of $g(x)$ will produce different convergence results.

Now we are ready to define the fixed point.

Definition of the fixed point: The value $x^{*}$ that satisfies this equation

(6) $\begin{align*}x^{*}=g(x^{*})\end{align*}$

is called the fixed point of $g(x)$ . Since the expression (6) is obtained from the nonlinear equation $f(x)=0$ , the fixed point is also the solution of the equation

(7) $\begin{align*}f(x^{*})=0\end{align*}$

The fixed point iteration is a method for iteratively computing the fixed point $x^{*}$ that satisfies (6). The fixed point iteration algorithm approximates the fixed point by propagating the fixed point iteration:

(8) $\begin{align*}x_{k+1}=g(x_{k}),\;\; k=0,1,2,3,\ldots\end{align*}$

where for $k=0$ the iteration is initialized with an initial guess $x_{0}$ selected by the user. For sufficiently large $k$ , $x_{k}$ approximates the fixed point $x^{*}$ .

The main questions are

When we can use the fixed point iteration to approximate the solution?
What are the conditions that the function 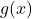$g(x)$ needs to satisfy such that the fixed point iteration converges?

Conditions on the function g(x) such that the fixed point iteration converges: Let us assume that

The function 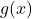$g(x)$ is continuously differentiable on some interval $[a,b]$ .
The function 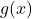$g(x)$ is such that $g(x)\in [a,b]$ for $\forall x\in [a,b]$ .
There exists a constant 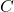$C$ , such that 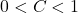$0< C <1$ and such that

(9) $\begin{align*}|\frac{\text{d}g(x)}{\text{d}x}|\le C, \;\; \forall x\in (a,b)\end{align*}$

That is, the constant $C$ is a constant that bounds the first derivative of $g(x)$ .

Then, the series of points $x_{1},x_{2},x_{3},\ldots$ generated by the fixed point iteration (8) converge to the fixed point $x^{*}$ for any initial guess $x_{0}$ in the interval $[a,b]$ . Furthermore, $x^{*}\in [a,b]$ .

Python Implementation of the Fixed Point Iteration

Here, we present a Python implementation of the fixed point iteration. The convergence error is measured by

(10) $\begin{align*}e=|x_{k+1}-x_{k}|\end{align*}$

As a demonstration, we consider the following example:

(11) $\begin{align*}f(x)=x^{2}+3x+2\end{align*}$

We consider the two forms of the function

(12) $\begin{align*}g(x)=\frac{-x**2-2}{3}\end{align*}$

and

(13) $\begin{align*}g(x)=-\sqrt{-3x-2}\end{align*}$

The accuracy of the final value is measured by computing

(14) $\begin{align*}f(x_{k})\end{align*}$

The closer the value $f(x_{k})$ to zero, the more accurate the solution is.

The Python implementation of the fixed point iteration is given below.

# -*- coding: utf-8 -*-
"""

Python implementation of the fixed point iteration
Author: Aleksandar Haber 

"""

import numpy as np 

# f function
def fFunction(x):
    y=x**2+3*x+2
    return y 

# g function 
# first version
def gFunction(x):
    y=(1/3)*(-x**2-2)
    return y

# g function 
# second version 
def gFunction2(x):
    y=-np.sqrt(-3*x-2)
    return y



# function implementing the fixed point iteration
def fixedPointIteration(gF,initialGuess, toleranceError =10**(-6), maxIteration=1000):
    #iteration 
    k=0
    # initialize the iteration
    x_k=initialGuess
    # initialize the error
    error=1000
    print("Iteration no: ", k, "** x= ", x_k)
    while(k<maxIteration and error>toleranceError):
        # fixed point iteration
        x_kp1=gF(x_k)
        error=np.abs(x_kp1-x_k)
        # update the variables
        x_k=x_kp1
        k=k+1
        print("Iteration no: ", k, "** x= ",x_k)
    return x_kp1
    
    
# initial guess 
x0= -1.5


# max number of iteration
maxIterationNumber=500

# tolerance error
tE=10**(-5)

# First g function

solution=fixedPointIteration(gFunction,x0, tE, maxIterationNumber)

# value of the function f
fFunction(solution)

# Second g function
# initial guess 
x0= -1.2

solution2=fixedPointIteration(gFunction2,x0, tE, maxIterationNumber)

# value of the function f
fFunction(solution2)

Basics of the Fixed Point Iteration

Python Implementation of the Fixed Point Iteration

admin

You might also like

How to Save Graphs to Image or PDF Files in Python by Using Pyplot and Matplotlib

Create Virtual Conda/Anaconda Python Environments in Linux and Install/Manage Packages

How to Properly Draw Circles in Python and Matplotlib