How to Solve Box and Inclined Plane Problem – Application of Newton’s Second Law Tutorial – Example 1 – Fusion of Engineering, Control, Coding, Machine Learning, and Science

In this physics and AP physics tutorial, we explain how to solve a box and inclined plane problem. More precisely, we will solve a problem related to Newton’s second law and the motion of an object up or down an inclined plane. This is the classical problem that in a more complex form appears in a number of engineering and aerospace applications. Consequently, it is very important to know how to accurately solve this problem and after reading this tutorial, you should think about real-life physical systems that can be modeled by this problem. Also, you should analyze the derived equations for the acceleration and reaction forces. By practicing this problem you can also prepare yourself for the Advanced Placement (AP) exams: AP Physics 1: Algebra-Based, AP Physics 2: Algebra-Based, AP Physics C: Mechanics, AP Calculus AB – Physics, and Advanced Placement (AP) Calculus.

Here is the problem formulation.

A box of mass $m$ is pulled by a force $F$ up an inclined plane. The angle of the inclined plane is $30$ degrees. If the coefficient of the kinetic friction between the box and the plane is $\mu$ , determine

(1) Normal reaction force that the plane is exerting on the box.
(2) Acceleration of the box.

This problem is illustrated in the figure below.

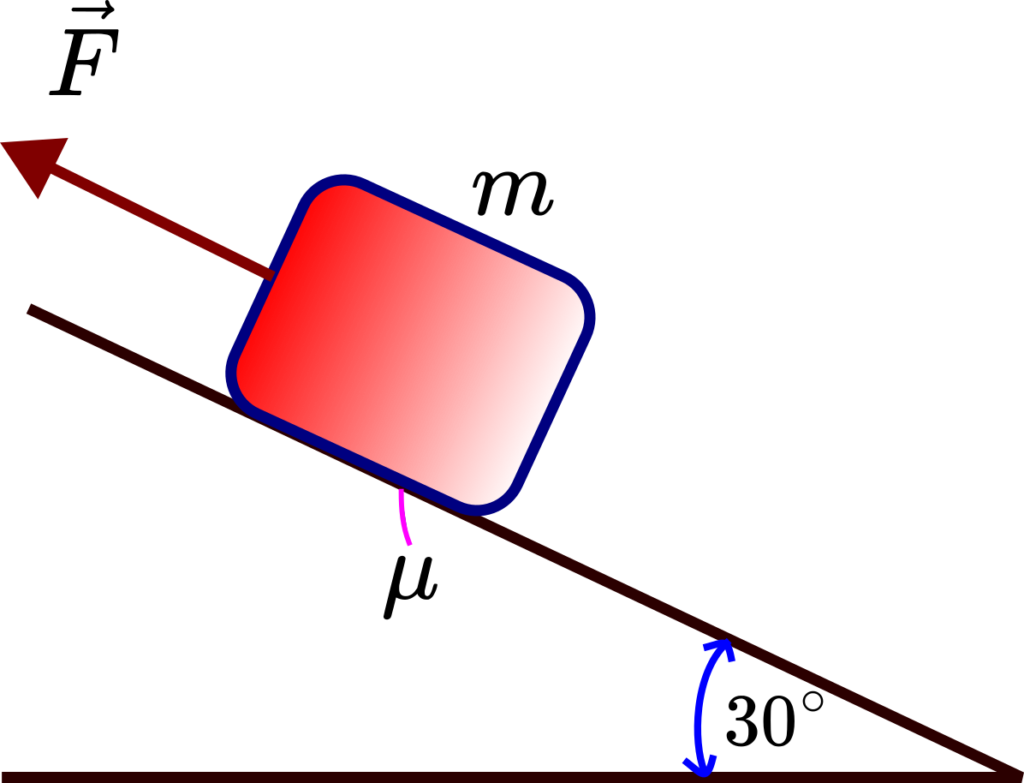
Figure 1: The box on the inclined plane.

The problem is solved by performing several steps. In the first step, we construct a free-body diagram and introduce the coordinate system. The free-body diagram and the coordinate system are given in the figure below.

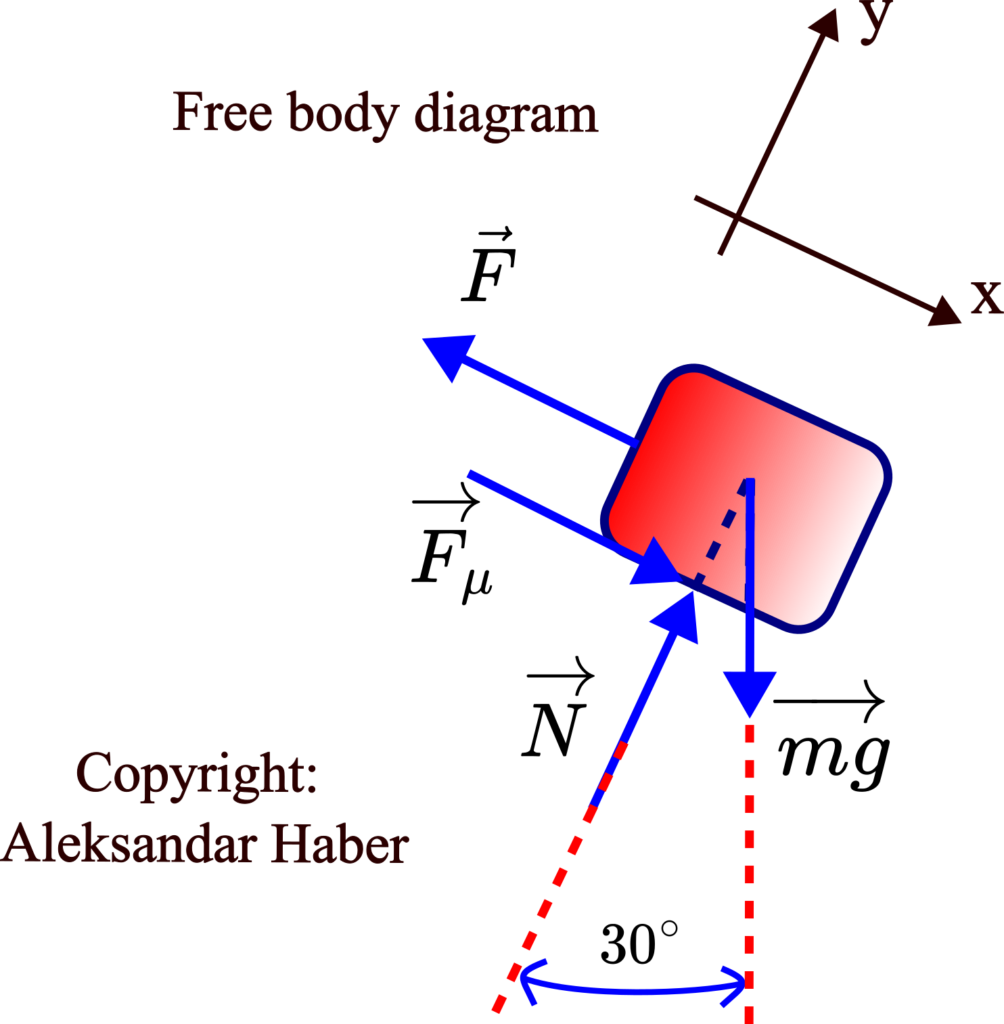
Figure 2: Free body diagram of the problem.

Here is the explanation of the forces:

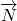$\overrightarrow{N}$ is the normal reaction force.
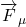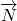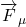$\overrightarrow{F}_{\mu}$ is the friction reaction force. This force direction is determined by the fact that this force opposes the direction of the motion. According to the problem formulation, the box moves up the inclined plane, and consequently, the friction force is acting in the opposite direction. Both $\overrightarrow{N}$ and $\overrightarrow{F}_{\mu}$ are the reaction forces.
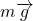$m\overrightarrow{g}$ is the weight of the box, and 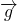$\overrightarrow{g}$ is the gravitational acceleration.
$\overrightarrow{F}$ is the external pull force that acts on the box.

Next, we construct a kinetic diagram shown in the figure below.

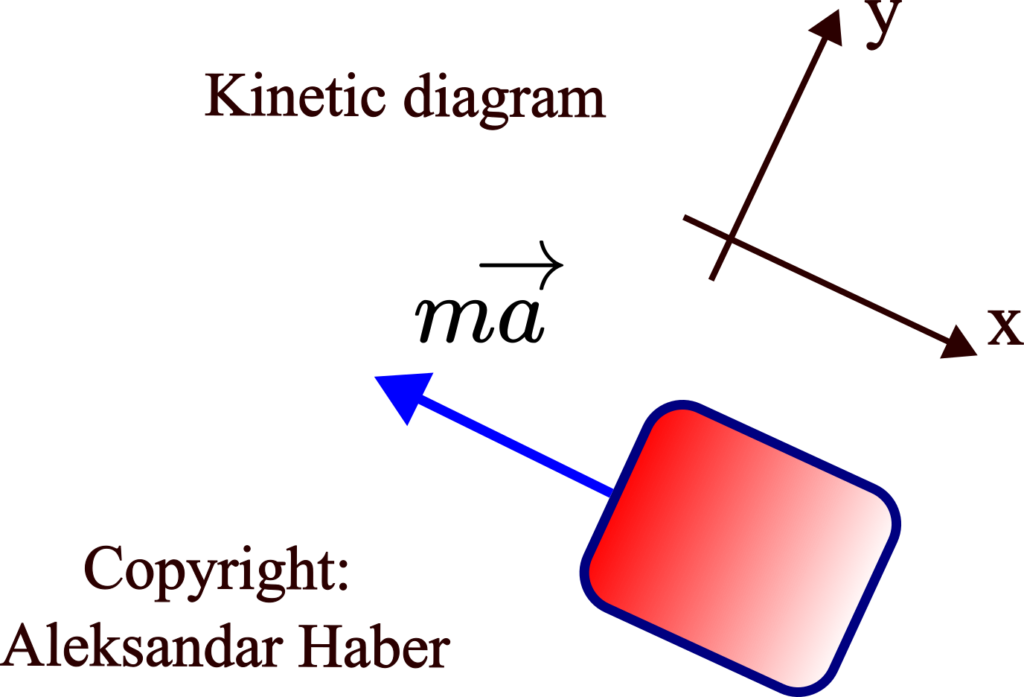
In the kinetic diagram, it was easy to specify the acceleration direction. Namely, from the text of the problem (problem statement), we know that the pulling force will pull the box up the inclined plane. Due to this and under some mild assumptions (that will not be introduced here for simplicity and brevity of this tutorial), this implies that the direction of the acceleration $\overrightarrow{a}$ will be in the direction of the pulling force.

In the next step, we apply Newton’s second law:

(1) $\begin{align*}m\overrightarrow{a}=\overrightarrow{F}+\overrightarrow{F}_{\mu}+\overrightarrow{N}+m\overrightarrow{g}\end{align*}$

This is a vector equation. Next, we need to project this equation onto the $x$ and $y$ axes. By projecting the equation (1) onto the $x$ axis, we obtain

(2) $\begin{align*}-ma=-F+F_{\mu}+mg\sin(30)\end{align*}$

On the other hand, the friction force $F_{\mu}$ can be expressed as follows

(3) $\begin{align*}F_{\mu}=N \cdot \mu\end{align*}$

By substituting this equation in the equation (2), and by using the fact that $\sin(30)=\frac{1}{2}$ , we obtain

(4) $\begin{align*}-ma=-F+N \cdot \mu+\frac{mg}{2}\end{align*}$

By projecting the equation (1) onto the y axis, we obtain

(5) $\begin{align*}0=N-mg\cos(30)\end{align*}$

By using the fact that $\cos(30)=\frac{\sqrt{3}}{2}$ , from the equation (5), we obtain

(6) $\begin{align*}N=mg\frac{\sqrt{3}}{2}\end{align*}$

The equation (6) solves the point 1. of the problem. By substituting (6) in (4), we obtain

(7) $\begin{align*}-ma & =-F+mg\mu \frac{\sqrt{3}}{2}+\frac{mg}{2} \\ma & =F-mg\mu \frac{\sqrt{3}}{2}-\frac{mg}{2}\\ma &=F-\frac{mg}{2}\big(1+\mu \sqrt{3} \big) \end{align*}$

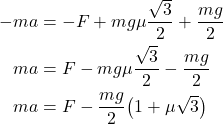
From the last equation, we obtain

(8) $\begin{align*}a=\frac{F}{m}-\frac{g}{2}\big(1+\mu\sqrt{3} \big) \end{align*}$

This is the solution 2 of the problem.

admin

You might also like

Free Fall of an Object (Ball) With Aerodynamic Drag Force

Determine the Resultant of Two Forces Making Arbitrary Angles – Solved Problem

How To Solve Projectile Motion Problem – Derivation of Kinematic and Dynamics Equations