In this C/C++ tutorial, you will learn:
- What is a bit-wise logical AND operator in C/C++
- What is a bit shift operator in C/C++
- How to transform integers into a binary form in C/C++. For example, you will learn how to transform an integer
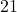 into its binary 8-bit form. The result is
into its binary 8-bit form. The result is  .
.
The main motivation for creating this post comes from the coding of microcontrollers and FPGAs. Namely, in microcontrollers and FPGAs, registers are used to store a bit pattern. On the other hand, in the high-level coding languages that are used to program microcontrollers and FPGAs, integer representations of bit patterns are used. Consequently, if you want to program your microcontroller or an FPGA by using C/C++, it is very important to know how to transform integers into a series of bits. The YouTube tutorial accompanying this page is given below.
Bit Representation of Unsigned Integers
Let us assume that we want to represent an unsigned integer as an 8-bit binary number. For example, let us consider the number 21. This number has the following binary representation:
(1) 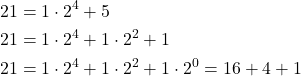
From the last expression, we have that:
- The bit at the position (0+1) is equal to
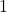
- The bit at the position (2+1) is equal to
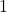
- The bit at the position (4+1) is equal to
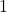
where the position is measured from the right (from the least significant bit) and all the other bits are equal to zero. This gives us the following binary representation of the number ![]()
(2) ![]()
Bit-wise logical AND
Bit-wise logical AND is best explained by using an example. Consider two numbers in the binary representation
(3) ![]()
As its name suggests, the bit-wise logical AND is applied element-wise. This operator is denoted by ![]() . We have
. We have
(4) ![]()
That is, we take the bits of ![]() and
and ![]() with the same significance (with the same position), and we apply a logical AND to these bits.
with the same significance (with the same position), and we apply a logical AND to these bits.
Bit Shift Operator in C/C++
Next, we explain the bit shift operator in C/C++. The left bit shift operator is denoted by ![]() . It is a binary operator that shifts the bits of the left operand for the number of bits represented by the right operand. For example, consider the following binary number
. It is a binary operator that shifts the bits of the left operand for the number of bits represented by the right operand. For example, consider the following binary number ![]() . The results of applying the following operation on
. The results of applying the following operation on ![]() is
is
(5) ![]()
In the same manner, we can define the right bit shift operator ![]() .
.
Transformation of Integers to Binary Numbers in C/C++
Now that we know what are bit-wise AND and bit shift operator, we can explain how to transform an unsigned integer to a binary number. First, we need to observe that a binary number with only a single non-zero bit can uniquely be represented by using a binary number with only a least significant bit and a shift operator. For example
(6) 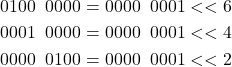
Now, let us consider the number ![]() in the decimal base. Its binary representation is
in the decimal base. Its binary representation is ![]() . We will show that we can create this binary representation by only using the number
. We will show that we can create this binary representation by only using the number ![]() , left bit shift operator, and the bit-wise logical AND operator. Consider the following operation
, left bit shift operator, and the bit-wise logical AND operator. Consider the following operation
(7) ![]()
This will obviously produce
(8) ![]()
This means that A has a non-zero bit at position 1 (least significant bit). Here it should be emphasized that in C/C++ A is usually declared as an unsigned integer. If we apply ![]() , C/C++ considers
, C/C++ considers ![]() as a binary number, although it is originally declared as an unsigned integer.
as a binary number, although it is originally declared as an unsigned integer.
On the other hand, consider the number ![]() . Its binary representation is
. Its binary representation is ![]() . Then we have,
. Then we have,
(9) ![]()
This means that ![]() has a zero bit at the position 1 (least significant bit). From this, we conclude
has a zero bit at the position 1 (least significant bit). From this, we conclude
IF ( (NUMBER ![]()
![]() ) ==
) == ![]() )
)
THEN NUMBER has 1 at the position of the first bit, OTHERWISE it has 0 at the position of the first bit.
where NUMBER is an unsigned integer. In this way, we can extract the bit at the first position. Note here again that NUMBER is declared as an unsigned integer in C/C++, and C/C++ internally considers it as a binary number while performing bit-wise logical operations. Let us go back to our original example of the number A, and let us explain how to extract the bit at the second position. Obviously, we have
(10) ![]()
This is because ![]() does not have 1 bit at the second position. On the other hand, the last expression can be written as follows
does not have 1 bit at the second position. On the other hand, the last expression can be written as follows
(11) ![]()
That is, we can use the left bit shift operator and ![]() to perform this logical statement. This generalized to
to perform this logical statement. This generalized to
IF ( (NUMBER ![]() (
(![]() )) == (
)) == (![]() ) )
) )
THEN NUMBER has 1 at the position of the second bit, OTHERWISE it has 0 at the position of the second bit.
In this way, we can extract the second bit.
In the general case, we have
IF ( (NUMBER ![]() (
(![]() )) == (
)) == (![]() ) )
) )
THEN NUMBER has 1 at the position of the ![]() th bit, OTHERWISE it has 0 at the position of the
th bit, OTHERWISE it has 0 at the position of the ![]() th bit.
th bit.
In this way, we can extract the ![]() th.
th.
That is, we learned that by only using AND, left shift bit operators, and ![]() we can transform integer representations into binary representations.
we can transform integer representations into binary representations.
C/C++ code
Here is the C/C++ code to perform the transformation.
#include <stdio.h>
#include <stdint.h>
int main()
{
uint8_t a;
uint8_t shiftedNumber;
uint8_t result;
uint8_t oneConstant=1;
bool bitValue;
a=55;
printf("%u \n",a);
for (unsigned int i=8;i>0;i--)
{
shiftedNumber=oneConstant<<(i-1); // shift 1 (i-1) places, for example i=8, 1<<(7) = 1000 0000
result = a & shiftedNumber; // this will return shiftedNumber if a has the bit that is equal to the non-zero bit of shiftedNumber
bitValue = (result==shiftedNumber) ? 1 : 0;
printf("%d",bitValue);
}
}
This code will produce ![]() , and that is exactly the 8-bit representation of the input number
, and that is exactly the 8-bit representation of the input number ![]() . The code is self-explanatory, except for the data type
. The code is self-explanatory, except for the data type ![]() . This is an unsigned 8-bit integer that is defined in the header file “stdint.h”. The explanation of this header file is given here.
. This is an unsigned 8-bit integer that is defined in the header file “stdint.h”. The explanation of this header file is given here.