In this post, we briefly revise the basic principles of statics and we apply them to compute the reaction forces of a beam.
We revise the basic principles by solving the following problem.
Problem: A beam of the length 2L is supported at point A by a roller support and at point B by a pin support (hinge support). At point C located at the distance L from the point A, there is a force F acting. The force F makes an angle of ![]() degrees with respect to the x axis. Compute the reaction forces at points A and B.
degrees with respect to the x axis. Compute the reaction forces at points A and B.
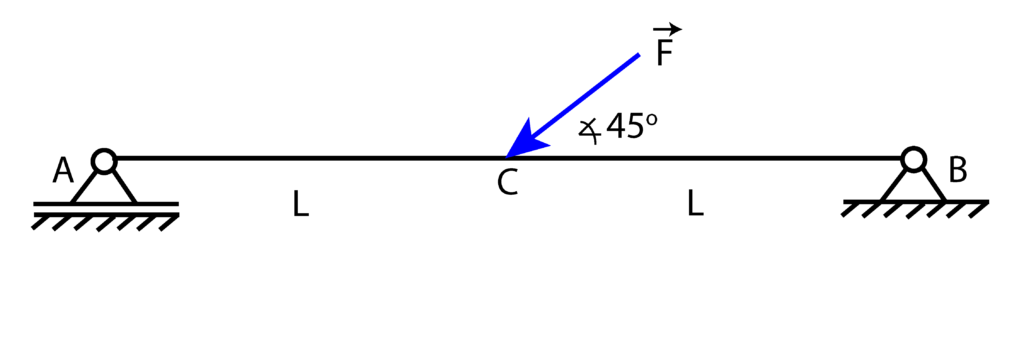
Solution: The first step is to identify quantities that are given. In our case, these quantities are the force F, angle of 45 degrees, and the distance L. The next step is to identify the quantities that need to be computed. These quantities are the reaction forces at points A and B. These quantities have to be computed as functions of the force F. In order to solve this problem, we need to construct a free-body diagram. We need to recall the direction of the reaction forces for the roller and the pin. An excellent overview of the types of supports in mechanical and civil engineering is given over here.
We know that the line of action of the roller reaction force is perpendicular to the contact plane. However, the sign of the reaction force (does it act up or down the line of action) is usually unknown, so we need to assume it. In certain scenarios, it is easy to accurately estimate the sign of the reaction force. In the case of the pin support, we do not know the direction of the reaction force. Consequently, we decompose the reaction force into two orthogonal directions. These directions are the projections of the reaction force.
The free-body diagram is given below.
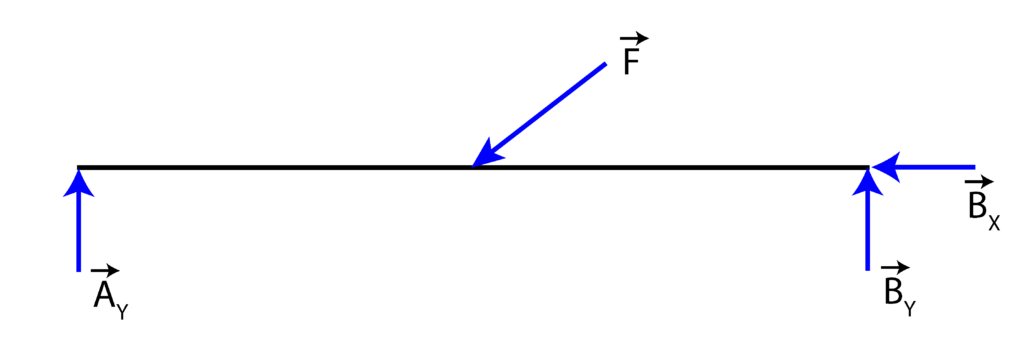
The reaction force ![]() acts in the vertical direction Y, and the reaction force at the pin B is decomposed into two projections
acts in the vertical direction Y, and the reaction force at the pin B is decomposed into two projections ![]() and
and ![]() .
.
To compute the reaction forces at points A and B, we need to recall the basic laws of statics. The basic question is:
When is a body in static equilibrium?
Well, students usually answer that a body is in static equilibrium if the sum of all the forces acting on the body is equal to zero. However, this is generally not true for bodies. This is true for a particle. Namely, the necessary and sufficient conditions for a particle to be in static equilibrium is:
A particle is in equilibrium if and only if the resultant of all the forces acting on the particle is equal to zero.
Note that the forces acting on a particle are concurrent, meaning that all the action lines of the forces pass through the same point.
In the case of rigid bodies, the situation is a bit more complex. The forces do not need to pass through the same point. The example below shows the case where the forces can be reduced to a point, and the resultant of these forces is zero, however, the system is not in the equilibrium
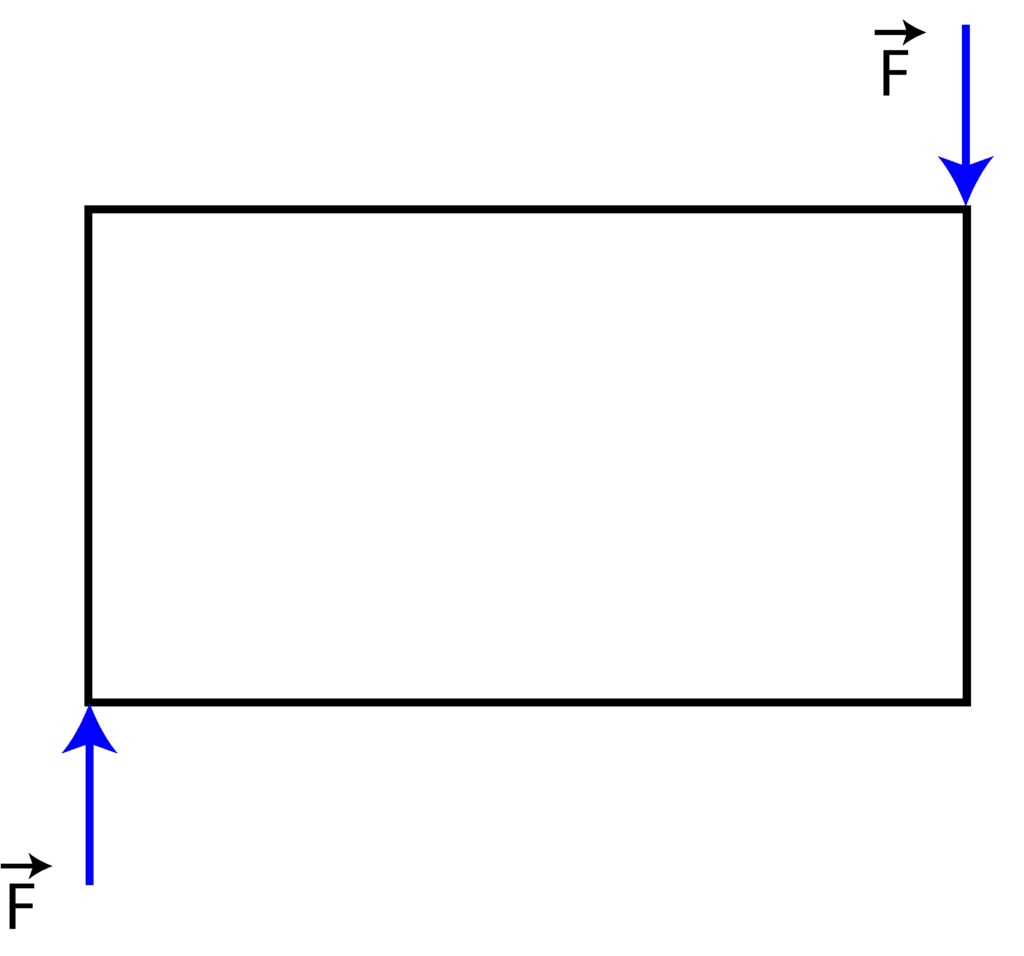
From statics, we know that a system of forces acting on the body can be reduced to resultant acting at a point and a moment of a couple (called moment resultant). Consequently, the condition for the static equilibrium of rigid bodies is that the resultant force is equal to zero and that the moment resultant is equal to zero. This condition can be mathematically expressed as follows
(1) ![]()
where the moments can be computed for any point. In two dimensions in the plane, these conditions reduce to
(2) ![]()
So let us go back to our problem. The first static equilibrium equation has the following form:
(3) 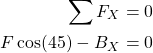
From this equation, we obtain the reaction force ![]()
(4) ![]()
The second equation has the following form
(5) 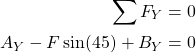
This equation reduces to the following equation
(6) ![]()
This equation has two unknowns, and consequently, it cannot be uniquely solved.
The third equation is the moment equation. We write the moment equation for point B. The choice of the point is arbitrary for this example. However, in some other examples, by wisely choosing the point, we can significantly simplify the moment equation. For example, is several unknown reaction forces are acting at a point, then this point should be chosen as a point for which the moment equation should be written. For the moment equation, we need to assume the moment signs. If the moment of the force revolves in the clockwise direction, then the moment is negative. On the other hand, if the moment of the force revolves in the counter-clockwise direction, then the sign of the moment is positive. The moment equation is
(7) 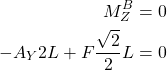
From this equation, we obtain
(8) ![]()
By substituting (8) in (6), we obtain the rection force ![]()
(9) 
We can verify this equation, by checking the moment equation for point A. Let us write the equation for point A
(10) ![]()
By substituting (9) in (10), we obtain
(11) ![]()
This equation is satisfied. Consequently, the results are correct.