MATLAB and Simulink Implementation of Sliding Mode Controller for Nonlinear Systems – Fusion of Engineering, Control, Coding, Machine Learning, and Science

In this control engineering and control theory tutorial, we explain how to implement a sliding mode controller for a nonlinear system in MATLAB and Simulink. We mainly focus on the implementation and we briefly discuss the theory behind the sliding mode control algorithm. As a demonstration and as a proof of the implementation principle, we consider a nonlinear pendulum system. The YouTube tutorial is given below.

Sliding Mode Control of Nonlinear Pendulum Model

The pendulum system is shown below.

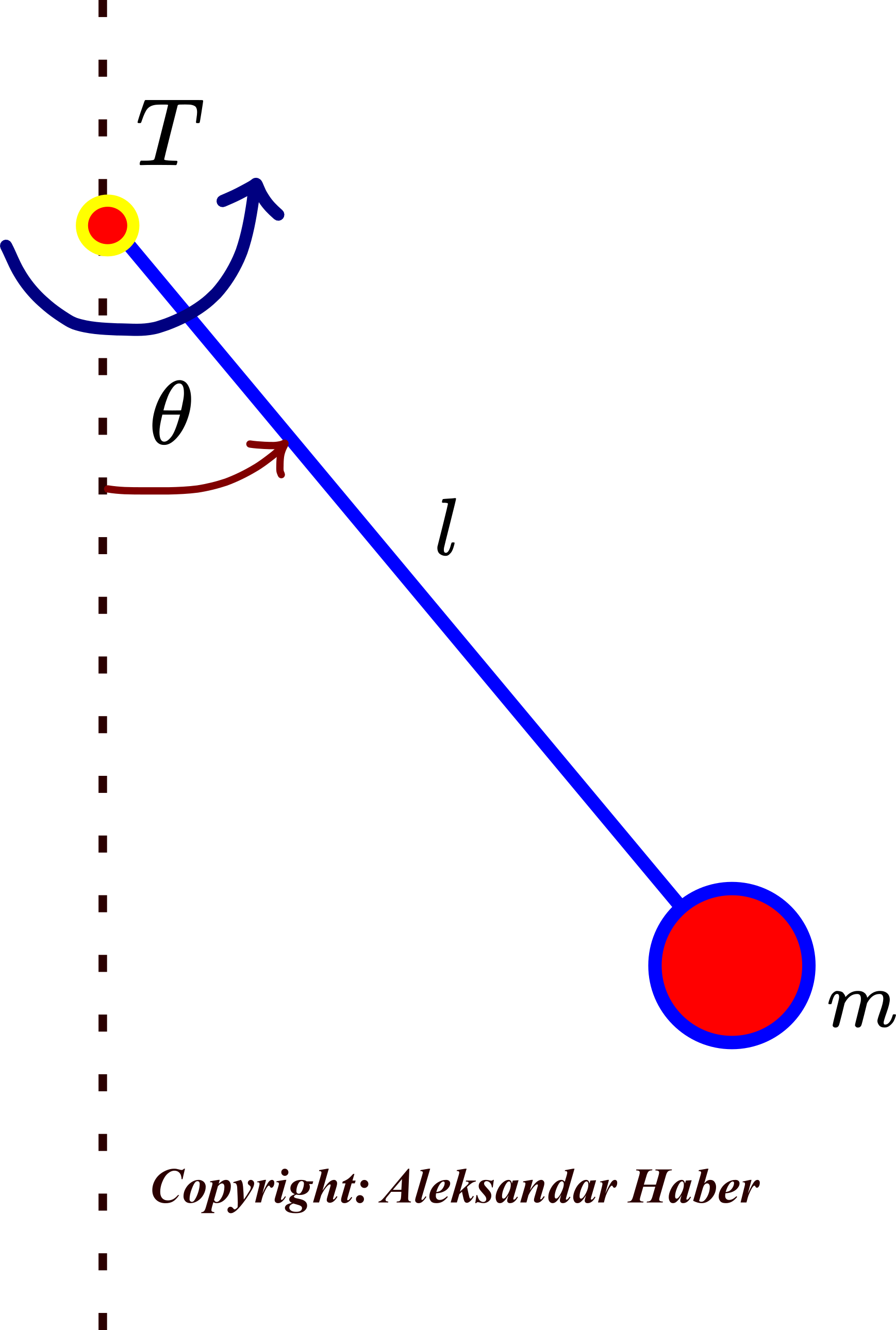
The mass of the ball is $m$ . The length of the rod (bar or beam) is $l$ . The angle $\theta$ defines the angle of rotation of the rod. We assume that the angle of rotation $\theta$ is controlled by using the torque $T$ acting at the suspension point. We neglect friction in the suspension bearings and the air resistance.

By using Newton’s second law, we obtain a differential equation describing the dynamics of the pendulum system

(1) $\begin{align*}\ddot{\theta}=-\frac{g}{l}\cdot \sin (\theta)+\frac{1}{ml^{2}}\cdot T\end{align*}$

Next, we introduce the following notation

(2) $\begin{align*}a=\frac{g}{l},\;\; b=\frac{1}{ml^{2}},\;\; u=T\end{align*}$

Consequently, the model looks like this

(3) $\begin{align*}\ddot{\theta}=-a\sin (\theta)+bu\end{align*}$

The control objective is to design a controller and a sequence of control inputs $u$ (torque sequence) that will make sure that the angle of rotation $\theta(t)$ follows a desired angle (reference trajectory) denoted by $\theta_{D}(t)$ .

We solve this problem by using the sliding mode controller. First, we introduce the tracking error $\varepsilon$

(4) $\begin{align*}\varepsilon = \theta_{D}-\theta\end{align*}$

The first and second derivatives of the tracking error are defined below

(5) $\begin{align*}\dot{\varepsilon} = \dot{\theta}_{D}-\dot{\theta} \\\ddot{\varepsilon} = \ddot{\theta}_{D}-\ddot{\theta}\end{align*}$

Secondly, we define the switching function (sliding function) as follows

(6) $\begin{align*}\sigma=c\varepsilon+\dot{\varepsilon}\end{align*}$

where $c$ is a positive parameter selected by the user.

The sliding mode control is computed by using the following equation:

(7) $\begin{align*}u=\frac{1}{b} \Big(c\dot{\varepsilon} +\ddot{\theta}_{D}+k\text{sgn}(\sigma) \Big)\end{align*}$

where $k$ is a design parameter selected by the user, and $\text{sgn}(\cdot)$ is a sign function. The parameter $k$ is a control tuning parameter. There is a minimal value of this parameter that ensures that the closed-loop system is stable and that the sliding motion and sliding mode are achieved by the controller. In the sequel, we show that if

(8) $\begin{align*}k>a\end{align*}$

then, the controller achieves sliding mode and sliding motion. That is, the equation (8) defines the minimal value of the parameter $k$ for the control system to work properly.

We need to show the following

(9) $\begin{align*}\sigma \cdot \dot{\sigma} \le -\eta |\sigma|\end{align*}$

where $\eta$ is a positive scalar. The condition (9) is often referred to as the reachability condition. The reachability condition ensures that the sliding mode is achieved in finite time and it guarantees that the controller will work.

First, let us take the first derivative of the switching function $\sigma$ defined in (6):

(10) $\begin{align*}\dot{\sigma}=c\dot{\varepsilon}+\ddot{\varepsilon}\end{align*}$

On the other hand, by substituting the second equation from (5) (the second derivative of the tracking error) in (10), we obtain

(11) $\begin{align*}\dot{\sigma}=c\dot{\varepsilon}+\ddot{\theta}_{D}-\ddot{\theta}\end{align*}$

Next, by substituting the dynamics (3) in (11), we obtain

(12) $\begin{align*}\dot{\sigma}=c\dot{\varepsilon}+\ddot{\theta}_{D}+a\sin (\theta)-bu\end{align*}$

Let us now substitute the control law (7) in (12). As a result, we obtain

(13) $\begin{align*}\dot{\sigma} & =c\dot{\varepsilon}+\ddot{\theta}_{D}+a\sin (\theta)-b \cdot \frac{1}{b} \Big(c\dot{\varepsilon} +\ddot{\theta}_{D}+k\text{sgn}(\sigma) \Big) \\\dot{\sigma} & =c\dot{\varepsilon}+\ddot{\theta}_{D}+a\sin (\theta) - c\dot{\varepsilon} - \ddot{\theta}_{D}-k\text{sgn}(\sigma) \\\dot{\sigma} & =a\sin (\theta)-k\text{sgn}(\sigma)\end{align*}$

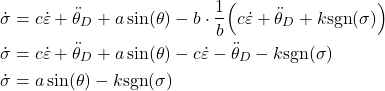
Next, by multiplying the last equation by $\sigma$ , we obtain

(14) $\begin{align*}\sigma \cdot \dot{\sigma} = a\sigma \sin (\theta)-k\sigma \text{sgn}(\sigma)\end{align*}$

Next, we use the following two equations:

(15) $\begin{align*}& \sigma \text{sgn}(\sigma) = |\sigma| \\& \sigma \sin (\theta) \le |\sigma|\end{align*}$

The last equation follows from the fact that the $\sin(x)$ function is always smaller than or equal to $1$ . From (14) and (15), we get

(16) $\begin{align*}\sigma \cdot \dot{\sigma} & \le a |\sigma| -k|\sigma| \\\sigma \cdot \dot{\sigma} & \le |\sigma| \big(a-k \big) \end{align*}$

From the last equation, we see that if

(17) $\begin{align*}a-k < 0\end{align*}$

or equivalently

(18) $\begin{align*} k>a\end{align*}$

Then, the reachability condition is satisfied with $\eta =k-a$ . This means that the control parameter $k$ should be selected such that

(19) $\begin{align*}k>a\end{align*}$

MATLAB and Simulink Implementation of Sliding Mode Control Algorithm

First of all, we create a MATLAB script that defines the model parameters.

% system parameters
g=9.81;
m=5;
l=1;
a=g/l;
b=1/(m*(l^2));
c=3;
k=2*a;

theta0=pi/6;
dtheta0=0.1;

The last two parameters called “theta0” and “dtheta0” are initial conditions for simulating the dynamics. The Simulink block diagram is shown below.

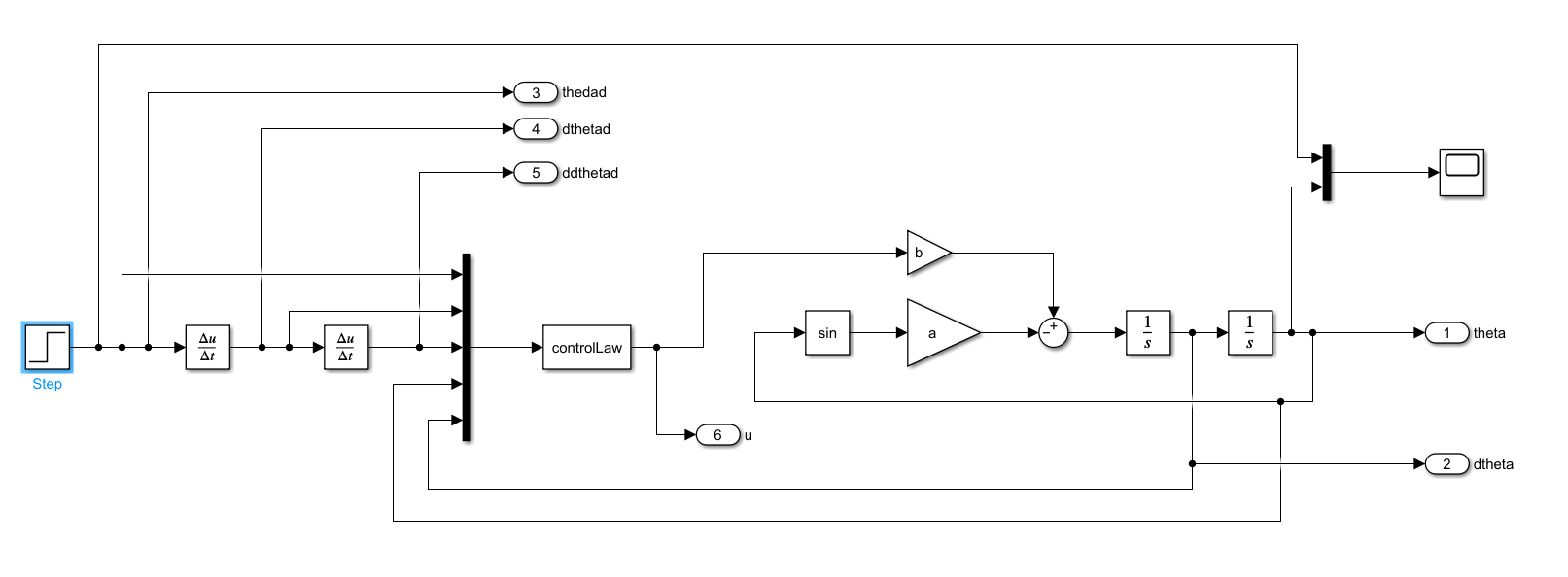
The dynamics is modeled by using the sin, two gain (a and b), sum, and two integrator blocks. The initial conditions are specified in the integrator blocks

The reference (desired) trajectory is a step signal. We also compute the first and second derivatives of the reference trajectory. We use the Mux block to group all the signals in a vector. This vector is passed to the MATLAB s-function block that implements the control law. The m-script called “controlLaw.m” implements the control law:

function [sys,x0,str,ts,simStateCompliance] = controlLaw(t,x,u,flag,b,k,c)
switch flag,

  case 0,
    [sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes;
  case 1,
    sys=mdlDerivatives(t,x,u);

  case 2,
    sys=mdlUpdate(t,x,u);

  case 3,
    sys=mdlOutputs(t,x,u,b,k,c);

  case 4,
    sys=mdlGetTimeOfNextVarHit(t,x,u);

  case 9,
    sys=mdlTerminate(t,x,u);

   otherwise
    DAStudio.error('Simulink:blocks:unhandledFlag', num2str(flag));

end


function [sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes

sizes = simsizes;

sizes.NumContStates  = 0;
sizes.NumDiscStates  = 0;
sizes.NumOutputs     = 1;
sizes.NumInputs      = 5;
sizes.DirFeedthrough = 1;
sizes.NumSampleTimes = 1;   % at least one sample time is needed

sys = simsizes(sizes);

x0  = [];

str = [];

ts  = [0 0];

simStateCompliance = 'UnknownSimState';

function sys=mdlDerivatives(t,x,u)

sys = [];

function sys=mdlUpdate(t,x,u)

sys = [];

function sys=mdlOutputs(t,x,u,b,k,c)
% u(1) - theta_d reference trajectory (desired trajectory)
% u(2) - derivative of theta_d
% u(3) - second derivative of theta_d
% u(4) - theta
% u(5) - derivative of theta

error=u(1)-u(4);
derror=u(2)-u(5);

sigma=c*error+derror;

control=(1/b)*(c*derror+u(3)+k*sign(sigma));

sys = control;


function sys=mdlGetTimeOfNextVarHit(t,x,u)

sampleTime = 1;    %  Example, set the next hit to be one second later.
sys = t + sampleTime;


function sys=mdlTerminate(t,x,u)

sys = [];

The parameters of the s-function block are shown below.

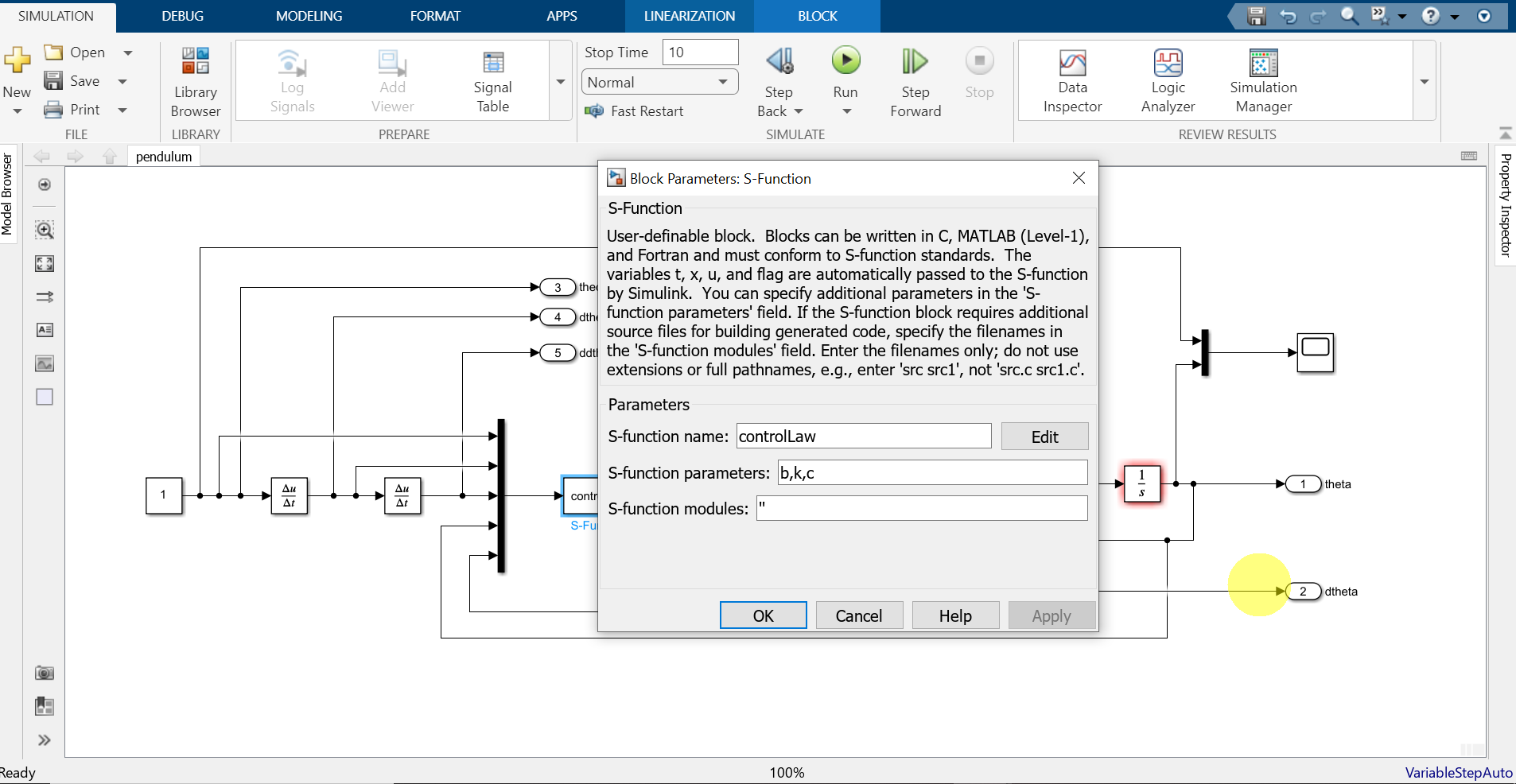
We use the outport blocks to export all the variables to the MATLAB workspace. The code below is used to plot the results once the variables are exported to the MATLAB workspace.

<pre class="wp-block-syntaxhighlighter-code">
% theta
theta=out.yout{1}.Values.Data;
% derivative of theta 
dtheta=out.yout{2}.Values.Data;
% thetad - desired value
thetad=out.yout{3}.Values.Data;
% first derivative of thetad
dthetad=out.yout{4}.Values.Data;
% second derivative of thetad
ddthetad=out.yout{5}.Values.Data;
% control input
u=out.yout{6}.Values.Data;

% error
e=thetad-theta;
% first derivative of error
de=dthetad-dtheta;

% define the sigma line
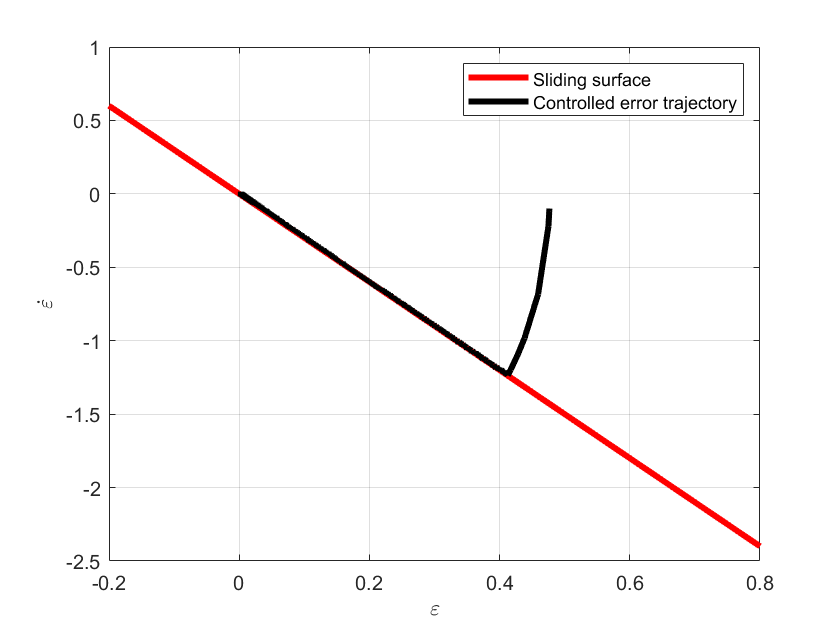
xLine=-0.2:0.01:0.8;
yLine=-c*xLine;

% switching function
sigma=c*e+de;


figure(1)
hold on
grid
box
plot(xLine,yLine,'r',LineWidth=3)
plot(e,de,'k',LineWidth=3)
xlabel('<img src="https://aleksandarhaber.com/wp-content/ql-cache/quicklatex.com-305d0239fb65087cbb5b6ccd24cec1ce_l3.png" class="ql-img-inline-formula quicklatex-auto-format" alt="&#123;&#92;&#118;&#97;&#114;&#101;&#112;&#115;&#105;&#108;&#111;&#110;&#32;&#125;" title="Rendered by QuickLaTeX.com" height="8" width="8" style="vertical-align: 0px;"/>','interpreter','latex','FontWeight','bold')
ylabel('<img src="https://aleksandarhaber.com/wp-content/ql-cache/quicklatex.com-d2c09514f46156d1d7aa802280b8bbbe_l3.png" class="ql-img-inline-formula quicklatex-auto-format" alt="&#123;&#92;&#100;&#111;&#116;&#123;&#92;&#118;&#97;&#114;&#101;&#112;&#115;&#105;&#108;&#111;&#110;&#125;&#125;" title="Rendered by QuickLaTeX.com" height="12" width="8" style="vertical-align: 0px;"/>','interpreter','latex','FontWeight','bold')
legend('Sliding surface','Controlled error trajectory')


figure(2)
hold on
grid 
box
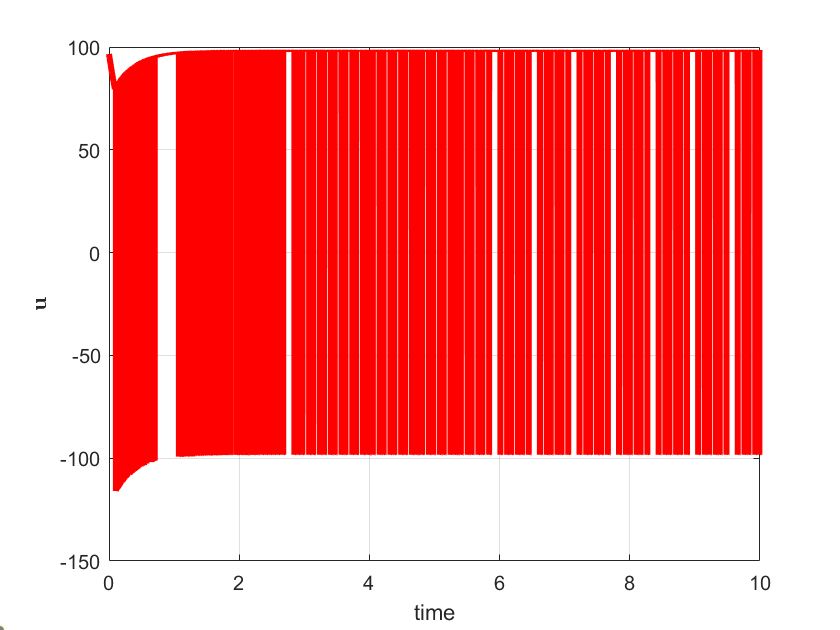
plot(out.tout,u,'r',LineWidth=3)
xlabel('time')
ylabel('<img src="https://aleksandarhaber.com/wp-content/ql-cache/quicklatex.com-b1eede20187d03f368a6ce744e1155f2_l3.png" class="ql-img-inline-formula quicklatex-auto-format" alt="&#123;&#92;&#109;&#97;&#116;&#104;&#98;&#102;&#123;&#117;&#125;&#125;" title="Rendered by QuickLaTeX.com" height="8" width="11" style="vertical-align: 0px;"/>','interpreter','latex','FontWeight','bold')

figure(3)
hold on
grid 
box 
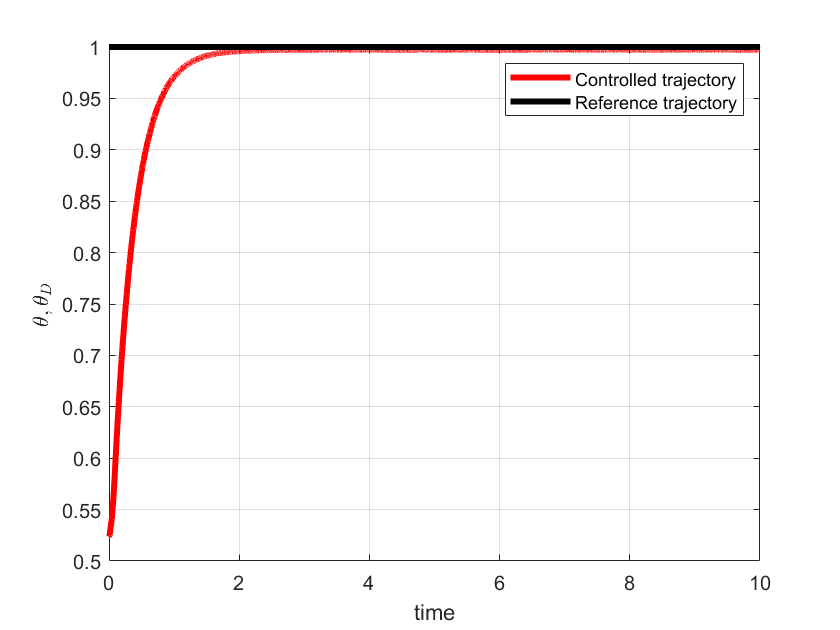
plot(out.tout,theta,'r',LineWidth=3)
plot(out.tout,thetad,'k',LineWidth=3)
xlabel('time')
ylabel('<img src="https://aleksandarhaber.com/wp-content/ql-cache/quicklatex.com-712c27de1b43423e8d2f7caccf11250d_l3.png" class="ql-img-inline-formula quicklatex-auto-format" alt="&#123;&#92;&#116;&#104;&#101;&#116;&#97;&#125;&#44;&#123;&#92;&#116;&#104;&#101;&#116;&#97;&#95;&#123;&#68;&#125;&#125;" title="Rendered by QuickLaTeX.com" height="16" width="36" style="vertical-align: -4px;"/>','interpreter','latex','FontWeight','bold')
legend('Controlled trajectory','Reference trajectory')

figure(4)
hold on 
grid 
box
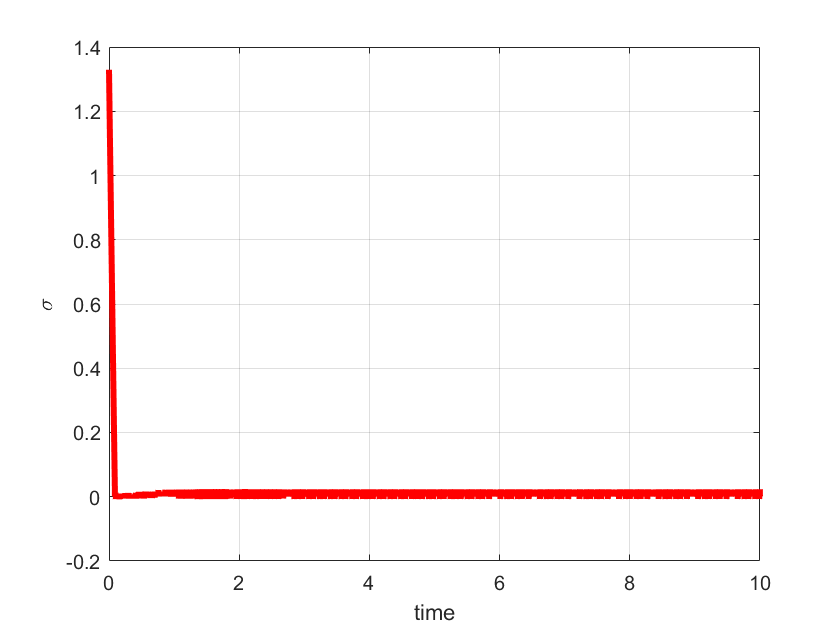
plot(out.tout,sigma,'r',LineWidth=3)
xlabel('time')
ylabel('<img src="https://aleksandarhaber.com/wp-content/ql-cache/quicklatex.com-1c9cc40f96a1492e298e7da85a2c1692_l3.png" class="ql-img-inline-formula quicklatex-auto-format" alt="&#92;&#115;&#105;&#103;&#109;&#97;" title="Rendered by QuickLaTeX.com" height="8" width="11" style="vertical-align: 0px;"/>','interpreter','latex','FontWeight','bold')


</pre>

The results are shown below.