In this tutorial, we will learn how to compute the Relative Strength Index (RSI) of stock time-series in Python. This indicator can be used to develop a trading strategy. The video accompanying this post is given here:
I realized that there are many websites that provide incomplete information on how this indicator is calculated. Furthermore, there are many websites that use inaccurate methods to compute this important indicator. Consequently, I had to consult the original work of J. Welles Wilder Jr. in which the RSI is defined. The name of the book is “New Concepts in Technical Trading Systems” and it was published in 1978. The Wikipedia page of J. Welles Wilder Jr says that he has a mechanical engineering background. To me, this does not come as a surprise since from my personal experience I know that mechanical engineers can apply their knowledge and developed intuition to various real-life problems.
So let us see how the RSI is being defined according to “New Concepts in Technical Trading Systems” (page 65, Section 6). Let ![]() be a stock closing-price time series. Let
be a stock closing-price time series. Let ![]() be a period for the computation of the RSI indicator.
be a period for the computation of the RSI indicator.
Step 1: Compute the price differences. That is, first we compute ![]() ,
, ![]() ,
, ![]() , etc. In the general case, the price difference is given by
, etc. In the general case, the price difference is given by ![]() .
.
Step 2: Compute the initial values for the RSI recuirsions. Let ![]() be time-series defined for
be time-series defined for ![]() as follows:
as follows:
(1) ![]()
Similarly, let ![]() be time-series defined for
be time-series defined for ![]() as follows:
as follows:
(2) ![]()
For example, if ![]() , and
, and ![]() ,
, ![]() , and
, and ![]() , we have:
, we have:
![]() ,
, ![]() , and
, and ![]()
and
![]() ,
, ![]() , and
, and ![]()
Next, we compute the averages of the time series ![]() and
and ![]() :
:
(3) ![]()
and
(4) ![]()
The relative strength is then computed as
(5) ![]()
where ![]() is the relative strength. Then, the RSI is computed as
is the relative strength. Then, the RSI is computed as
(6) ![]()
where ![]() is used to denote the RSI.
is used to denote the RSI.
Step 3. First, we initialize the following variables:
(7) 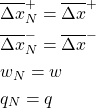
where ![]() ,
, ![]() ,
, ![]() and
and ![]() are computed in the initial step 2 explained above.
are computed in the initial step 2 explained above.
For ![]() , recursively compute
, recursively compute
(8) 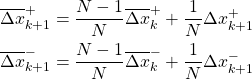
where
(9) 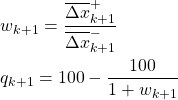
The above-explained computational steps, produce a time series of the RSI:
The code for computing the RSI is given below. We download the SPY stock (ETF) prices and we plot the closing price and the computed RSI.
# -*- coding: utf-8 -*-
"""
Compute Relative Strength Index (RSI) of stock time series in Python
Source:
“New Concepts in Technical Trading Systems” (page 65, Section 6).
by J. Welles Wilder Jr
Author:
Aleksandar Haber
Date: January 25, 2021
Some parts of this code are inspired by the following sources:
-- https://www.datacamp.com/community/tutorials/pickle-python-tutorial
-- Pandas help: https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.DataFrame.ewm.html
-- "Learn Algorithmic Trading: Build and deploy algorithmic trading systems and strategies
using Python and advanced data analysis", by Sebastien Donadio and Sourav Ghosh
"""
# standard imports
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
# used to download the stock prices
import pandas_datareader as pdr
# define the period parameter for RSI
period_RSI=14
# define the dates for downloading the data, the date difference should be
# larger than the RSI period
startDate= '2020-8-1'
endDate= '2021-2-3'
stock_symbol='SPY'
# download the data from Yahoo
data = pdr.get_data_yahoo(stock_symbol,start=startDate,end=endDate)
# inspect the data
data.head()
data['Close'].plot()
# isolate the closing price
closingPrice = data['Close']
differencePrice = data['Close'].diff()
differencePriceValues=differencePrice.values
positive_differences=0
negative_differences=0
current_average_positive=0
current_average_negative=0
price_index=0
RSI=[]
for difference in differencePriceValues[1:]:
if difference>0:
positive_difference=difference
negative_difference=0
if difference<0:
negative_difference=np.abs(difference)
positive_difference=0
if difference==0:
negative_difference=0
positive_difference=0
# this if block is used to initialize the averages
if (price_index<period_RSI):
current_average_positive=current_average_positive+(1/period_RSI)*positive_difference
current_average_negative=current_average_negative+(1/period_RSI)*negative_difference
if(price_index==(period_RSI-1)):
#safeguard against current_average_negative=0
if current_average_negative!=0:
RSI.append(100 - 100/(1+(current_average_positive/current_average_negative)))
else:
RSI.append(100)
# this is executed for the time steps > period_RSI, the averages are updated recursively
else:
current_average_positive=((period_RSI-1)*current_average_positive+positive_difference)/(period_RSI)
current_average_negative=((period_RSI-1)*current_average_negative+negative_difference)/(period_RSI)
#safeguard against current_average_negative=0
if current_average_negative!=0:
RSI.append(100 - 100/(1+(current_average_positive/current_average_negative)))
else:
RSI.append(100)
price_index=price_index+1
#create the RSI time series
RSI_series=pd.Series(data=RSI,index=data['Close'].index[period_RSI:])
# create the 30 and 70 limit lines
num_entries=RSI_series.values.size
line30=num_entries*[30]
line70=num_entries*[70]
# create the Pandas dataframe with 30 and 70 line limits
lines30_70=pd.DataFrame({'30 limit': line30, '70 limit': line70},index=RSI_series.index)
# plot RSI and prices on the same graph
with plt.style.context('ggplot'):
import matplotlib
font = { 'weight' : 'bold',
'size' : 14}
matplotlib.rc('font', **font)
fig = plt.figure(figsize=(20,20))
ax1=fig.add_subplot(211, ylabel='Stock price $')
data['Adj Close'].iloc[period_RSI:].plot(ax=ax1,color='r',lw=3,label='Close price',legend=True)
ax2=fig.add_subplot(212, ylabel='RSI')
RSI_series.plot(ax=ax2,color='k',lw=2,label='RSI',legend=True)
lines30_70['30 limit'].plot(ax=ax2, color='r', lw=4, linestyle='--')
lines30_70['70 limit'].plot(ax=ax2, color='r', lw=4, linestyle='--')
plt.savefig('RSI.png')
plt.show()
This code produces the following diagrams.
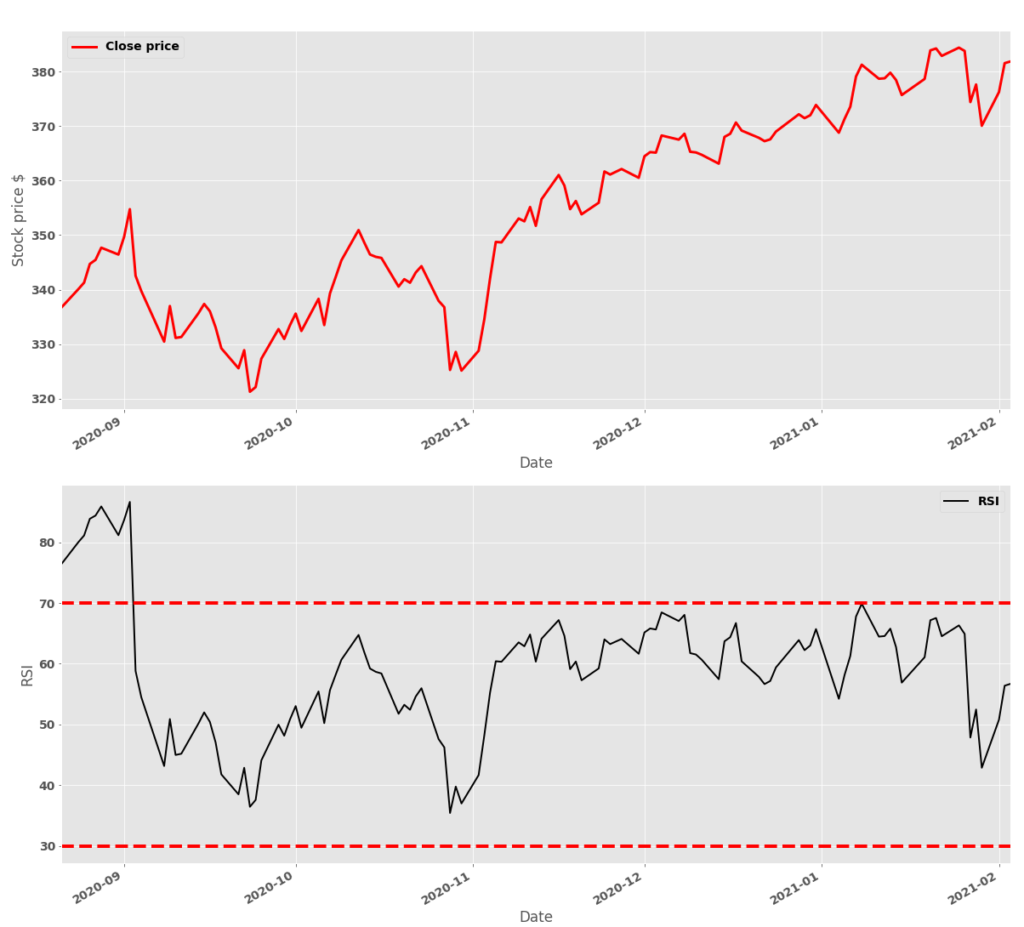
Figure 1 shows the closing price and the computed RSI. We also plot the 30 and 70 limits that are used as oversold/overbought limits.