In this Python scientific computing tutorial, we will learn how to solve systems of equations analytically by using Python’s symbolic library called SymPy. The technique that you will learn in this webpage tutorial is very important for analytically solving complicated nonlinear equations and for verifying solutions computed by hand. The YouTube tutorial accompanying this webpage tutorial is given below.
Everything explained in this tutorial applies to both linear and nonlinear algebraic equations, as long as the solution exists and the solution can be found in the closed analytical form. First of all, to solve the equations, they have to be transformed into the following form
(1) 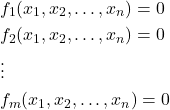
where ![]() are linear or nonlinear functions of the variables
are linear or nonlinear functions of the variables ![]() . For example, let us say that we want to solve this system of equations
. For example, let us say that we want to solve this system of equations
(2) 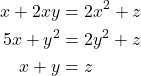
where ![]() and
and ![]() are the variables. This system has to be written like this
are the variables. This system has to be written like this
(3) 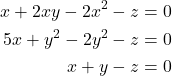
To explain how to solve systems of equations, let us consider this test case
(4) ![]()
In this formulation, we assume that the ![]() and
and ![]() are variables that we want to solve for, and
are variables that we want to solve for, and ![]() is a parameter. That is, we want to express the solution in the following form
is a parameter. That is, we want to express the solution in the following form
(5) ![]()
where ![]() and
and ![]() are the nonlinear functions that we want to determine. The first implementation step is to import the necessary Python libraries:
are the nonlinear functions that we want to determine. The first implementation step is to import the necessary Python libraries:
import numpy as np
from sympy import *
init_printing()
We need the NumPy library since we will substitute symbolic expressions at the end. Then, we import the complete SymPy library. Finally, we call SymPy’s function “init_printing()” which is used to generate nice prints of symbolic expressions.
Next, we define the symbolic variables ![]() ,
, ![]() , and
, and ![]() and define the system of nonlinear equations (4).
and define the system of nonlinear equations (4).
# create the symbolic x,y, and z variables
x,y,z=symbols('x y z')
# define two equations in the form f(x,y,z)=0
equation1=2*z+5*x*y+2*z*y+2
equation2=-2*x*z+5-3*z*y
We use the following code to solve the system of equations and to generate the solution in the human-readable form
# compute the result
solution=solve([equation1, equation2], x,y, dict=True)
# the result is stored in the variable called "solution"
# we have two sets of solution
# first set
# here is how we can get the x solution
simplify(solution[0][x])
# here is how we can get the y solution
simplify(solution[0][y])
# second set
# here is how we can get the x solution
simplify(solution[1][x])
# here is how we can get the y solution
simplify(solution[1][y])The solve the system of equations, we use SymPy’s function “solve()”. The first input argument is a list representing equations in the system. The second and third input arguments are variables that are unknowns in the system. In our case, the system needs to be solved for ![]() and
and ![]() , and
, and ![]() is the parameter. That is, the variable
is the parameter. That is, the variable ![]() is the parameter in the system. The variables
is the parameter in the system. The variables ![]() and
and ![]() will be expressed as functions of
will be expressed as functions of ![]() . The last input argument of the function “solve()” is a flag indicating that we want to return the solution in the form of a dictionary. We have two sets of solutions. The first set is accessed by calling “solution[0]” and the second set “solution[1]”. We access the “x” variable from the first set by using “simplify(solution[0][x])” and the “y” variable by using “simplify(solution[0][y])”.
. The last input argument of the function “solve()” is a flag indicating that we want to return the solution in the form of a dictionary. We have two sets of solutions. The first set is accessed by calling “solution[0]” and the second set “solution[1]”. We access the “x” variable from the first set by using “simplify(solution[0][x])” and the “y” variable by using “simplify(solution[0][y])”.
We simplify the computed solutions and access the variables ![]() and
and ![]() by typing
by typing
# here is how we can get the x solution
simplify(solution[0][x])
# here is how we can get the y solution
simplify(solution[0][y])The result is given below.
(6) 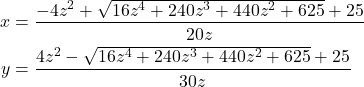
This is the solution from the first set. We can double-check that this is the solution by substituting the expressions for ![]() in
in ![]() in (4). We perform the substitutions by using the Python script shown below.
in (4). We perform the substitutions by using the Python script shown below.
# to verify the solution
# double check the first equation
eq1check=equation1.subs(x,solution[0][x]).subs(y,solution[0][y])
# we should get zero
eq1check=simplify(eq1check)
# double check the second equation
eq2check=equation2.subs(x,solution[0][x]).subs(y,solution[0][y])
# we should get zero
eq2check=simplify(eq2check)
The substituted expressions denoted by “eq1check” and “eq2check” are equal to zero. This means that the solution (6) is correct.
Next, let us compute the numerical values of the solutions ![]() and
and ![]() . We do that by using SymPy’s function “subs”:
. We do that by using SymPy’s function “subs”:
expressionX=solution[0][x]
expressionY=solution[0][y]
valueX=expressionX.subs(z,1)
valueY=expressionY.subs(z,1)The computed values for ![]() are
are
(7) 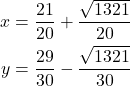
The result is nicely expressed as a symbolic fraction. However, we can compute a floating point value of the solution by using the script shown below.
valueXcomp=valueX.evalf(5)
valueYcomp=valueY.evalf(5)The result is
(8) ![]()