November 24, 2024
Calculus / Mathematics

Clear Explanation of Integration by Substitution – Part I

adminby admin


In this mathematics, calculus, and AP calculus tutorial, we explain how to solve integrals by substitution. In this first tutorial part, we solve the following three examples

(1)   \begin{align*}& \int e^{5x}\; \mathrm{d}x \\& \int \sqrt{2x+2} \; \mathrm{d}x \\& \int \frac{x}{\sqrt{1-2x^{2}}} \; \mathrm{d}x\end{align*}

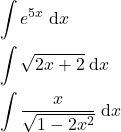
We first solve these examples in order for students to obtain an intuitive understanding of integration by substitution. In the second part of this tutorial, given here, we explain a general approach for solving integrals by substitution and we solve more complex examples. The YouTube video accompanying this mathematics and calculus tutorial is given below.

Solution of First Integral by Substitution

Let us first solve the first integral:

(2)   \begin{align*} \int e^{5x}\; \mathrm{d}x \end{align*}

Integration means that we want to find a function whose derivative is equal to the function under the integral. In our case, the function under the integral is e^{5x}. Consequently, we want to find a function whose derivative is equal to e^{5x}. Let us not recall this integral

(3)   \begin{align*} \int e^{t}\; \mathrm{d}t =e^{t} \end{align*}

Can we somehow use the integral (3) to solve (2)? Let us try with this substitution of variables

(4)   \begin{align*}t=5x \end{align*}

From this substitution, we have

(5)   \begin{align*}\frac{\mathrm{d}t}{\mathrm{d}x}= 5 \\\mathrm{d}t=5\mathrm{d}x\end{align*}

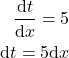
From the last equation, we have

(6)   \begin{align*}\mathrm{d}x=\frac{1}{5}\mathrm{d}t\end{align*}

By substituting (4) and (6) in (2), we obtain

(7)   \begin{align*} \int e^{5x}\; \mathrm{d}x & = \int e^{t}\; \frac{1}{5}\mathrm{d}t = \frac{1}{5} \int e^{t}\; \mathrm{d}t \\& = \frac{1}{5} e^{t}\end{align*}

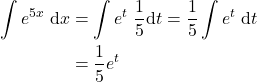
By substituting (4) in (7), we obtain find the solution of the integral

(8)   \begin{align*} \int e^{5x}\; \mathrm{d}x =\frac{1}{5} e^{5x}\end{align*}

It is always a good practice to verify this solution. We can verify this solution by taking the derivative of the function on the right-hand-side of the integral (8):

(9)   \begin{align*}\frac{\mathrm{d} }{\mathrm{d}x}\Big( \frac{1}{5} e^{5x} \Big) =\frac{1}{5} e^{5x} 5= e^{5x}\end{align*}

and that is precisely the function under the integral. This means that we have correctly solved the integral.

Solution of Second Integral by Substitution

Let us solve the second integral:

(10)   \begin{align*}\int \sqrt{2x+2} \; \mathrm{d}x \end{align*}

What should be the substitution here? Let us try this substitution

(11)   \begin{align*}t=2x+2\end{align*}

Let us take the derivative of t

(12)   \begin{align*}\frac{\mathrm{d}t }{\mathrm{d}x}=2 \end{align*}

From the last equation, we have

(13)   \begin{align*} \mathrm{d}x =\frac{1}{2}\mathrm{d}t \end{align*}

By substituting (11) and (13) in (10), we have

(14)   \begin{align*}\int \sqrt{2x+2} \; \mathrm{d}x & = \int \sqrt{t} \; \frac{1}{2}\mathrm{d}t = \frac{1}{2} \int \sqrt{t} \; \mathrm{d}t \\& =\frac{1}{2}\frac{t^{\frac{3}{2}}}{\frac{3}{2}}=\frac{1}{2}\cdot \frac{2}{3}t^{\frac{3}{2}}= \frac{1}{3}t^{\frac{3}{2}}\end{align*}

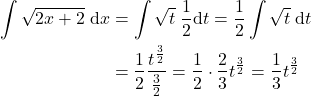
By substituting (11) in (14), we obtain the solution

(15)   \begin{align*}\int \sqrt{2x+2} \; \mathrm{d}x = \frac{1}{3}(2x+2)^{\frac{3}{2}}\end{align*}

Let us verify this result by computing the derivative of (15):

(16)   \begin{align*}\frac{\mathrm{d} }{\mathrm{d}x}\Big( \frac{1}{3}(2x+2)^{\frac{3}{2}} \Big)=\frac{1}{3}\cdot \frac{3}{2}\cdot (2x+2)^{\frac{1}{2}}\cdot 2 =\sqrt{2x+2}\end{align*}

This is exactly the function under the integral (10). This means that we have correctly solved the integral.

Solution of Third Integral by Substitution

Let us solve this integral

(17)   \begin{align*}\int \frac{x}{\sqrt{1-2x^{2}}} \; \mathrm{d}x \end{align*}

In this case, the substitution is

(18)   \begin{align*}t=1-2x^{2}\end{align*}

By taking the derivative of the last expression, we have

(19)   \begin{align*}\frac{\mathrm{d}t }{\mathrm{d}x}=-4x\end{align*}

From the last equation, we have

(20)   \begin{align*}x\mathrm{d}x=-(\frac{1}{4})\mathrm{d}t\end{align*}

By substituting (18) and (20) in (17), we have

(21)   \begin{align*}\int \frac{x}{\sqrt{1-2x^{2}}} \; \mathrm{d}x & = -\frac{1}{4}\cdot \int \frac{1}{\sqrt{t}} \; \mathrm{d}t = -\frac{1}{4} \int t^{-\frac{1}{2}} \; \mathrm{d}t \\& = -\frac{1}{4}\frac{t^{\frac{1}{2}}}{\frac{1}{2}}=-\frac{1}{4}\cdot 2 t^{\frac{1}{2}}=-\frac{1}{2}t^{\frac{1}{2}}\end{align*}

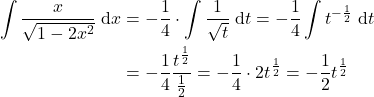
By substituting (18) in (21), we obtain the solution of the integral

(22)   \begin{align*}\int \frac{x}{\sqrt{1-2x^{2}}} \; \mathrm{d}x = -\frac{1}{2}(1-2x^{2})^{\frac{1}{2}}=-\frac{1}{2} \cdot \sqrt{1-2x^{2}} \end{align*}

To verify this, let us compute the derivative of (22):

(23)   \begin{align*}\frac{\mathrm{d} }{\mathrm{d}x}\Big( -\frac{1}{2}(1-2x^{2})^{\frac{1}{2}} \Big) = -\frac{1}{4}(1-2x^{2})^{-\frac{1}{2}} (-4x)=\frac{x}{\sqrt{1-2x^{2}}} \end{align*}

admin

View all posts by admin →

You might also like

Write Reciprocal (Inverse) of a Complex Number in Standard (Rectangular) Form

What is a Characteristic Polynomial of a Matrix?

Divide Complex Numbers – Detailed Explanation of How to Compute Complex Number Quotients with Python Verification