Write Reciprocal (Inverse) of a Complex Number in Standard (Rectangular) Form – Fusion of Engineering, Control, Coding, Machine Learning, and Science

In this calculus, algebra, and complex number tutorial, we will learn how to write the reciprocal of a complex number in the standard or rectangular form. We will also explain how to write a Python script that can be used to verify analytical computations. This tutorial is very important for mechanical and electrical engineering students interested in electrical circuits, signal processing, fluid mechanics, electrical networks, power systems, and control theory. The YouTube video tutorial is given below.

Problem Statement and Solution

We consider the following problem. Consider the following expression

(1) $\begin{align*}q=\frac{1}{3+2i}\end{align*}$

where $i$ is the imaginary unit. Provide the answer to the following question and solve the following problem

Is $q$ a complex number?
If YES, write this complex number in the standard (rectangular) form:
(2) $\begin{align*}q=a+bi\end{align*}$

where $a$ is a real part of $q$ and $b$ is the imaginary part of $q$ .

Solution. The expression (1) is a complex number. This will become clear after solving the problem. Generally speaking, a reciprocal of a complex number is a complex number. To solve the problem, we need to somehow transform the expression for $q$ into an expression in which the denominator will be a real number. To do that, we need to use one very simple idea. Namely, let $z=w+gi$ be a complex number with the real part $w$ and the imaginary part $g$ . Then if we multiply $z$ by its complex conjugate, we obtain the following expression

(3) $\begin{align*}(w+gi)(w-gi)=w^{2}-wgi+wgi-(gi)^{2}=w^{2}-(gi)^{2}\end{align*}$

The last expression can be written as follows

(4) $\begin{align*}(w+gi)(w-gi)=w^{2}-wgi+wgi-(gi)^{2}=w^{2}-(gi)^{2}=w^{2}+g^{2}\end{align*}$

From (4) we conclude that if we multiply a complex number by its complex conjugate, we will obtain a real number. This is important since we can use this trick to get rid of the complex number in the denominator of (1). Also, another thing should be observed. Namely, the expression (3) is very similar to the well-known expression for the difference of squares of two real numbers

(5) $\begin{align*}(s_{1}-s_{2})(s_{1}+s_{2})=s_{1}^{2}-s_{2}^{2}\end{align*}$

Let us now use this trick to solve the problem. From (1), we have

(6) $\begin{align*}q=\frac{1}{3+2i}\cdot \frac{3-2i}{3-2i}\end{align*}$

Over here, we multiplied both the numerator and denominator of $q$ with the complex conjugate of $3+2i$ . That is, with $3-2i$ . The idea is to get rid of the complex number in the denominator. As the result, from (7), we obtain

(7) $\begin{align*}q& =\frac{1}{3+2i}\cdot \frac{3-2i}{3-2i}=\frac{3-2i}{(3+2i)(3-2i)} \\& =\frac{3-2i}{3^{2}-(2i)^{2}}=\frac{3-2i}{9+4}=\frac{3-2i}{13} \\& = \frac{3}{13}-\frac{2}{13}i\end{align*}$

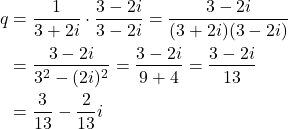
This solves our problem. The real part is given by $3/13$ and the imaginary part is given by $2/13$ .

Python Script for Computing Reciprocal of Complex Number

Here, we present a Python script for computing a reciprocal of a complex number. There are two approaches for computing the inverse complex number. The first approach is to use built-in Python complex number functions. The second approach is to use the SymPy Python library. The SymPy library is a Python symbolic computation library that is very useful for manipulating and simplifying complex expressions. The Python script is given below.

# -*- coding: utf-8 -*-
"""
Reciprocal of Complex Numbers

@author: Aleksandar Haber 
Date: November 2023
"""
# two approached for computing a reciprocal of a complex number
# Python 

# First approach - by using the built-in comple operations
# 1j is the standard notatio for the imaginary unit in Python 

R1=1/(3+2j)


# Second approach - by using SymPy 
# - symbolic Python library 
from sympy import *
init_printing() 

# I is the imaginary unit in SymPy
z1 = 3 + I*2

R2=1/z1

R3=simplify(R2)
R3
print(R3)

Problem Statement and Solution

Python Script for Computing Reciprocal of Complex Number

admin

You might also like

Clear Explanation of the Fixed Point Iteratin for Solving Nonlinear Equations and Python Implementation

Easy Introduction to Complex Numbers – Part 1

Complex Numbers in Python – Define, Perform Basic Operations, and Convert Polar Form to Rectangular and Vice-Versa