by
In this Python, calculus, and symbolic Python tutorial, we will learn how to compute, simplify, expand, and rewrite the symbolic algebraic and trigonometric expressions in Python. This tutorial is very important for people who want to master symbolic computation in Python. The YouTube tutorial accompanying this webpage tutorial is given below.
To perform operations on symbolic expressions, we use the SymPy Python library. This is a powerful Python library for performing operations on symbolic expressions. To install this library, you need to write in your command prompt or in the Anaconda prompt
pip install sympy
Let us start with the following simplifications. Below are the standard trigonometric expressions
(1) 
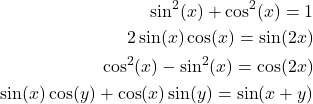
To simplify these expressions we use the function “simplify()”. But, first, we need to import the necessary packages and define the symbolic variables. We do that by using the following Python script:
from sympy import *
# x,y,z are symbolic variables
x, y, z = symbols('x y z')
# for nice printing
init_printing(use_unicode=True)
The first code line will import all the functions and packages from SymPy. Then, the code line “x, y, z = symbols(‘x y z’) ” will define three symbolic variables 
and 
. Then, the function “init_printing(use_unicode=True)” is used for nice printing.
The following Python script is used to simplify the expression given in Eq.(1):
# sin(x)**2+cos(x)**2=1
simplify(sin(x)**2+cos(x)**2)
# 2*sin(x)*cos(x)=sin(2x)
simplify(2*sin(x)*cos(x))
# cos(x)**2-sin(x)**2=cos(2x)
simplify(cos(x)**2-sin(x)**2)
# sin(x)*cos(y)+cos(x)*sin(y)=sin(x+y)
simplify(sin(x)*cos(y)+cos(x)*sin(y))
The simplify() function is a very powerful tool. For example, it can be used to simplify complex expressions such as this one
(2) 
To simplify this expression we can write in Python
simplify(4*sin(x)*cos(x)+2*(cos(x)**2-sin(x)**2))
However, the simplify() function cannot simplify this obvious expression:
(3) 
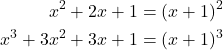
That is, if you try to execute these code lines
# watch out, it cannot simplify these expressions
simplify(x**2+2*x+1)
simplify(x**3+3*x**2+3*x+1)
you will not be able to simplify these expressions.
To be able to simplify these types and more complex types of expressions, we need to use the function “factor()”.
The function “factor()” is used to factorize the expressions and to significantly simplify them. We can type
factor(x**2+2*x+1)
factor(x**3+3*x**2+3*x+1)
To factorize the above expressions.
Another very useful function is the “expand()” function. The expand() function is used to expand the expressions and polynomials in Python. For example, let us expand this expression
(4) 
We can do that, like this
exp1=((x+1)**3)*(2*x+1)
# here we expand the expression,
exp2= expand(exp1)
The result is
(5) 
The functions expand() and factor() are inverses of each other. We can verify this by executing the following code that will expand the expression and then reverse the action of expand by factoring the expression
# expand the expression and factor it
exp1=((x+1)**3)*(2*x+1)
# here we expand the expression,
exp2= expand(exp1)
exp3=factor(exp2)
# we get zero and that is correct
exp1-exp3
Another very useful function to learn is rewrite(). This function will rewrite the expression in terms of the specific variable or a function. This function is especially useful for manipulating trigonometric expressions as we can see in the example shown below.
# we can also rewrite expressions, by using rewrite
# this is especially useful for trigonometrix expressions
exp4=sin(2*x)+cos(2*x)
exp4.rewrite(cos)
exp4.rewrite(sin)
