by
Consider the cantilever beam shown in Fig. 1 below.
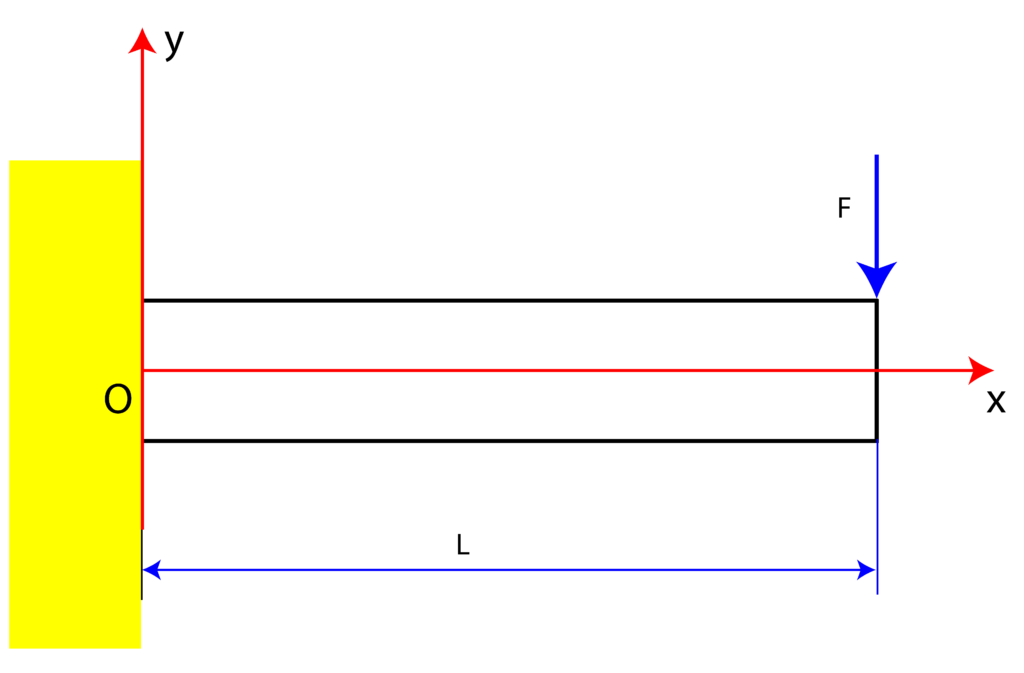
Note the location of the coordinate system center. Assume that length 
, force 
, modulus of elasticity 
, and moment of inertia 
are given.
a) Derive the equations of deformation 
.
b) For a chosen (realistic) values of , , , and , plot the function 
in MATLAB or in any other software that you know (Python, Mathematica).
Deadline: Friday, November 05, 2021, at 10:10 AM
IMPORTANT COMMENTS:
– Number of points: 5 points on the final exam (however, both a) and b) have to be completed successfully).
– During the lectures on Friday, we explained how to solve the bending differential equation to compute the deformation in the direction as a function of 
. However, the coordinate system center was different from the coordinate center location in Fig. 1. Consequently, the mathematical forms of equations will be different for two coordinate system locations.
