Move (Translate) Forces From One Point to Another

This brief lecture explains how to move (better to say “translate”) forces from one point to another. This is a useful technique for analyzing the static equilibrium of rigid bodies. The YouTube video accompanying this post is given below.

Basically, to make a long story short, a force acting at a certain point can be moved (without rotating the line of action of the force) to an arbitrary chosen point X if a couple is added whose moment is equal to the moment of the force around point X (X is the symbol for the point).

The main idea is to replace the force, with a force and a moment whose action on the body is equivalent to the action of the original force.

Equivalence of two force systems: Two force systems are equivalent if they result in the identical resultant force and the identical resulting moment.

So let us see how this works in practice.

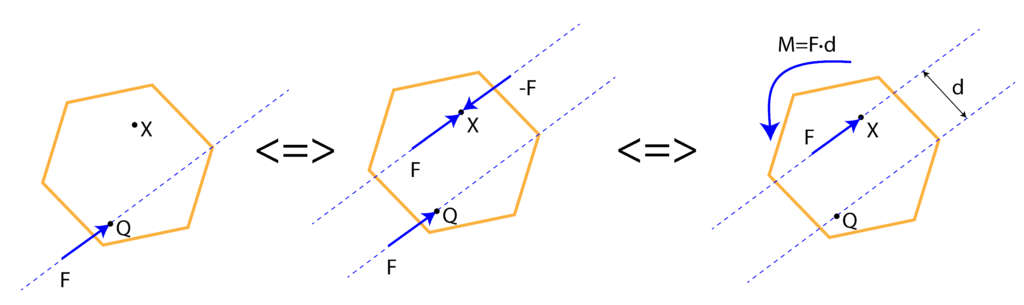
Consider the figure shown below. The goal is to “move” the force from the point to the point , where can be an arbitrary point.

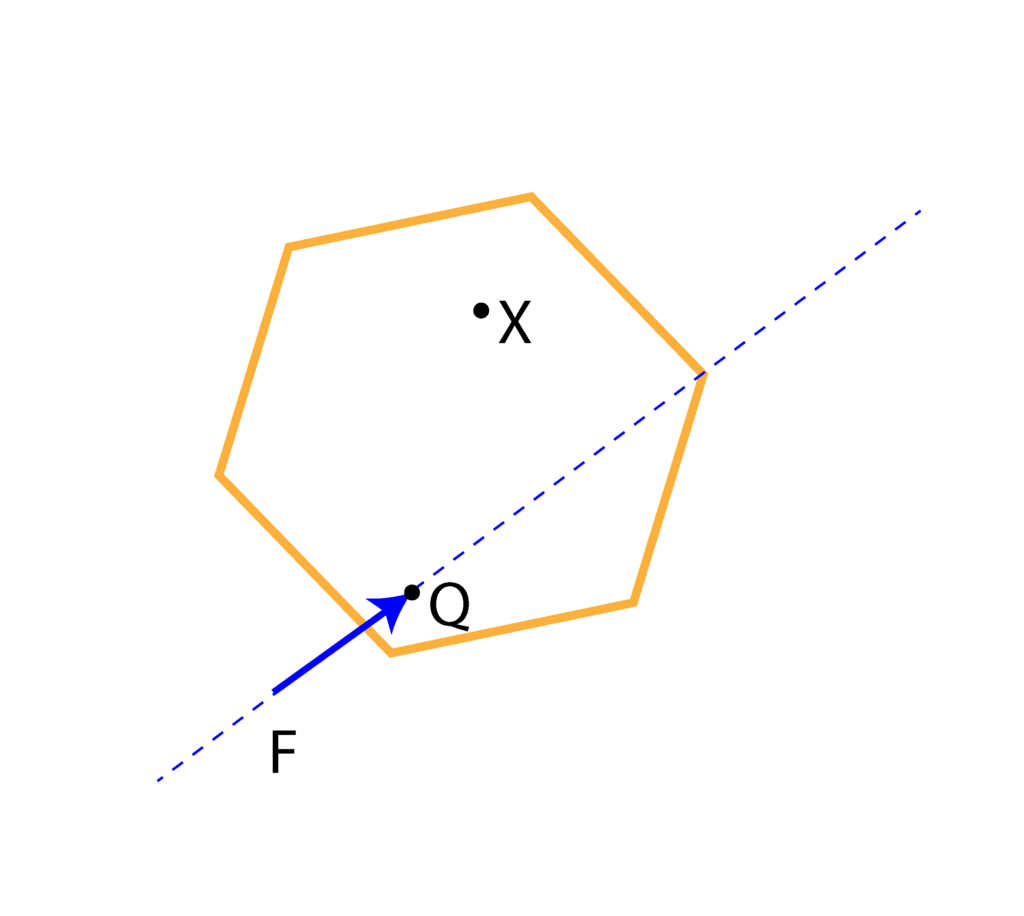
Now, we add two forces whose intensities are equal to the intensity of , and whose action lines are parallel to the action line of the force . The two forces that are added have to be of opposite signs in order not to disturb the original action of the force . That is, the two new forces can be canceled, however, we are not going to cancel them. Figure 2 below shows this.

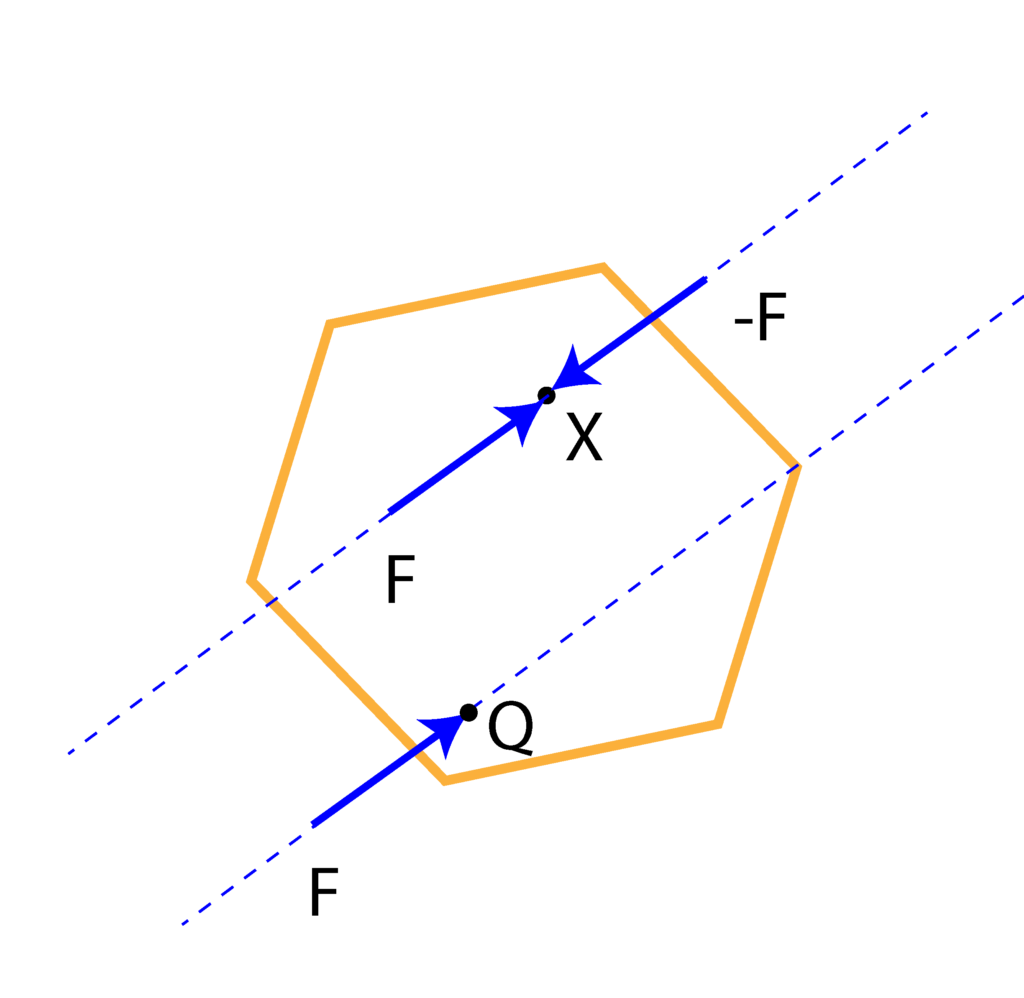
Now, it should be observed that the original force at the point and the force acting at the point , form a couple whose moment is equal to where is the shortest distance between the two parallel lines passing through and . This is shown in Fig. 3 below.

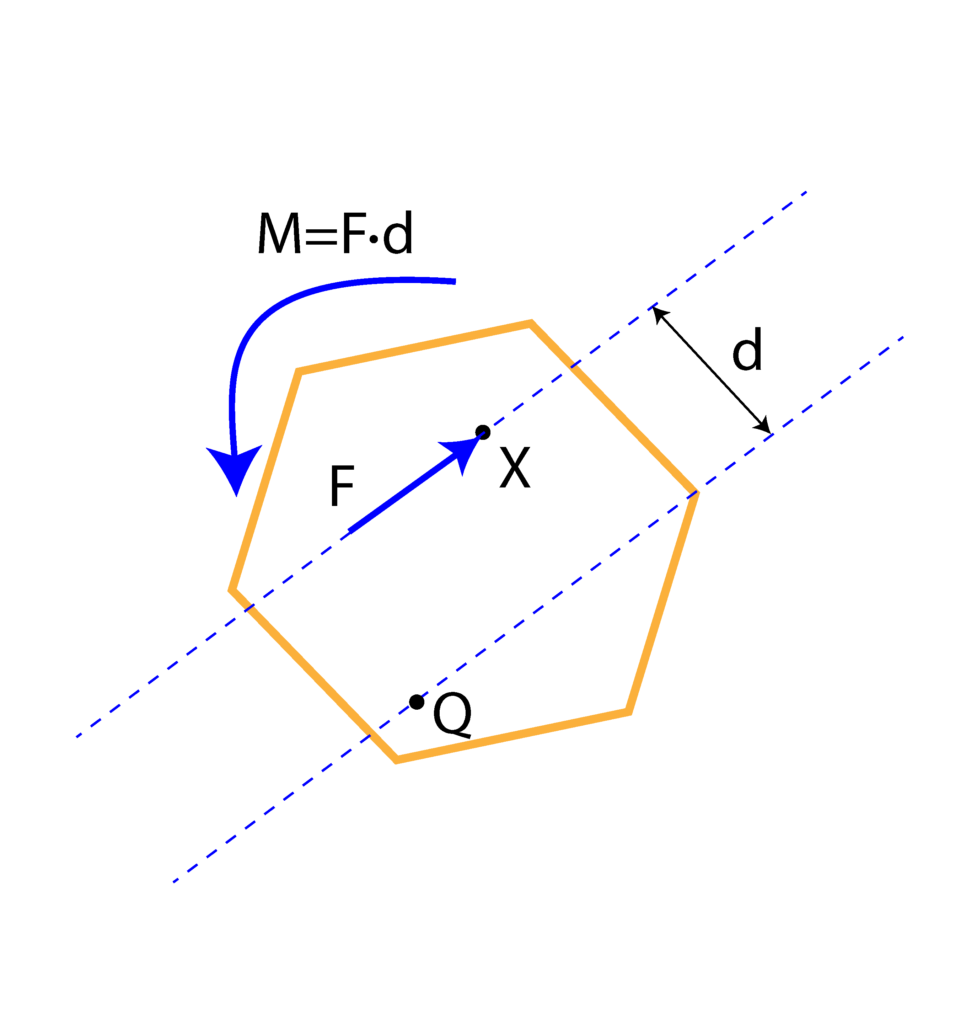
So, we have demonstrated the procedure for moving forces from one point to another. Under the condition that we add an additional moment of a couple, we can “safely” translate forces from one point to another.

What should be observed is that from the mechanics point of view, the situations in Figs. 1., 2., and 3. are equivalent. That is, the system of forces in Figs. 1, 2, and 3, are equivalent. This is symbolically illustrated by the following graph.