In this lecture, we introduce the concept of stress and the concept of normal stress. A YouTube video accompanying this lecture is given below.
Consider an element (member, or a mechanical part) shown in Fig. 1 below. An external axial force ![]() is acting on both sides of the element. We can safely assume that the weight of the element is much smaller than the applied external force (here, you should keep in mind that there is a difference between the weight and the mass of an object- what is the difference?). Now, let us perform a thought experiment that might not be realistic in practice, however, it can help us to better understand the concept of stress. Suppose that we are able to cut the element into two segments. Let us then ask ourselves the following question:
is acting on both sides of the element. We can safely assume that the weight of the element is much smaller than the applied external force (here, you should keep in mind that there is a difference between the weight and the mass of an object- what is the difference?). Now, let us perform a thought experiment that might not be realistic in practice, however, it can help us to better understand the concept of stress. Suppose that we are able to cut the element into two segments. Let us then ask ourselves the following question:
What are the conditions that will ensure that these two segments are in the static equilibrium?
Let us consider segment 1. Since there is an external force ![]() acting on the segment, there must be forces that counter act this force that keep this segment in the static equilibrium. Otherwise, the object will fly away pulled by the force
acting on the segment, there must be forces that counter act this force that keep this segment in the static equilibrium. Otherwise, the object will fly away pulled by the force ![]() . Indeed, there are forces that resist the action of the external forces. These forces are called internal forces, and they are actually induced by the external force
. Indeed, there are forces that resist the action of the external forces. These forces are called internal forces, and they are actually induced by the external force ![]() . From the physical point of view, these internal forces are forces that one layer of material exerts on another layer of material (relate this to Newton’s third law). In our case, shown in Fig. 1, the internal forces of segment 1, are actually the forces that segment 2 is exerting on segment 1. Under the condition that the imaginary cut is relatively far away from the action point of the force
. From the physical point of view, these internal forces are forces that one layer of material exerts on another layer of material (relate this to Newton’s third law). In our case, shown in Fig. 1, the internal forces of segment 1, are actually the forces that segment 2 is exerting on segment 1. Under the condition that the imaginary cut is relatively far away from the action point of the force ![]() , we can safely assume that internal forces are uniformly distributed (they have equal magnitudes as shown in Fig. 1 below). You can also think of springs that connect segments 1 and 2. Once the external force
, we can safely assume that internal forces are uniformly distributed (they have equal magnitudes as shown in Fig. 1 below). You can also think of springs that connect segments 1 and 2. Once the external force ![]() is applied, the spring will expand, and there will be internal forces in the spring.
is applied, the spring will expand, and there will be internal forces in the spring.
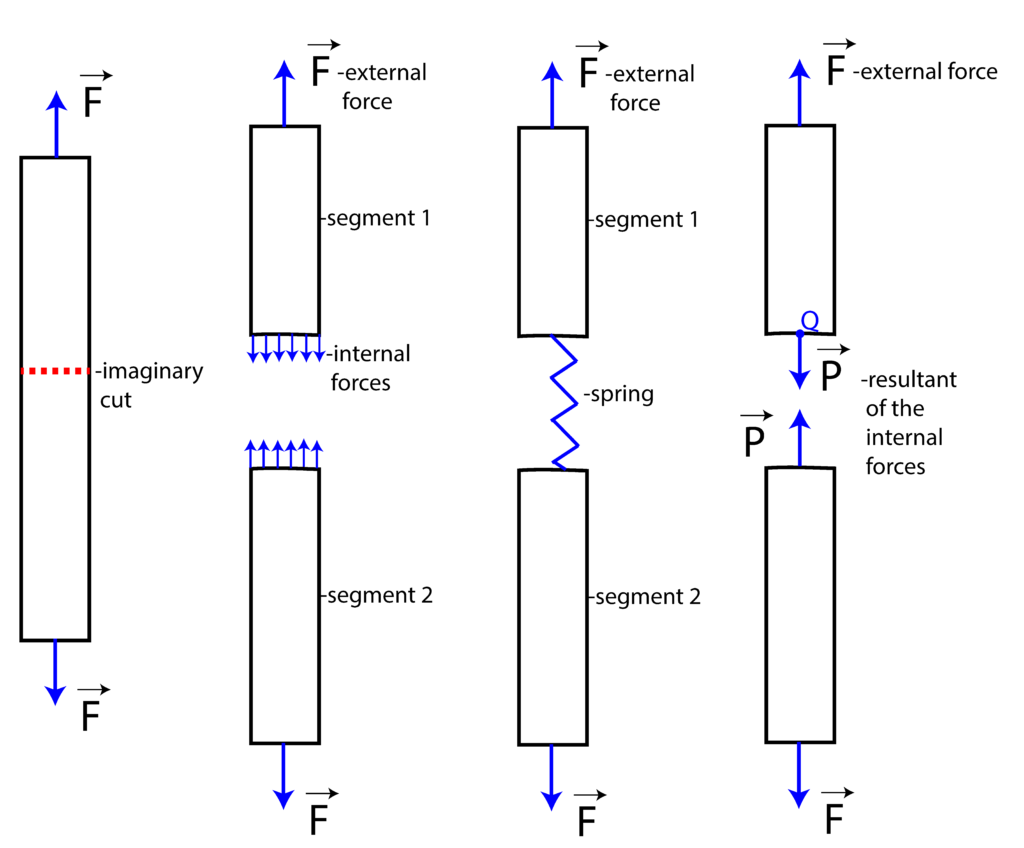
Let us now consider again segment 1. From basic laws of statics, it follows that an internal force acting at an arbitrary point can be moved (translated) to point Q (and an additional moment of a couple needs to be added). This force translation is explained over here in more detail.
By moving all the internal forces to point Q, and by summing these forces, we obtain a resultant of the internal forces. Note here, that the moments of internal forces that result from internal forces translation to Q will cancel each other due to the assumption that the internal forces are uniform and equal. This resultant force is denoted by ![]() . Since the element is in the static equilibrium, its every segment and piece is in equilibrium. Consequently, the segments 1 and 2 are in static equilibrium. For segment 1 to be in equilibrium, the following condition needs to be satisfied
. Since the element is in the static equilibrium, its every segment and piece is in equilibrium. Consequently, the segments 1 and 2 are in static equilibrium. For segment 1 to be in equilibrium, the following condition needs to be satisfied
(1) ![]()
That is, the intensities of the forces ![]() and
and ![]() are equal. That is
are equal. That is ![]() .
.
In this particular example, we assumed that the distribution of internal forces is uniform. This assumption is justified if the imaginary cut is relatively far away from the action point of the external force. In this case, normal stress is defined by
(2) ![]()
where ![]() is the cross-section area of the element and
is the cross-section area of the element and ![]() is the normal stress symbol. The stress unit is Newton per meter squared, that is
is the normal stress symbol. The stress unit is Newton per meter squared, that is ![]() . Stress is called normal since the internal force is perpendicular to the cross-section. In reality, the cross-section can assume any shape. For example, we can have a cylindrical object, with a circular cross-section. This case is illustrated in the figure below.
. Stress is called normal since the internal force is perpendicular to the cross-section. In reality, the cross-section can assume any shape. For example, we can have a cylindrical object, with a circular cross-section. This case is illustrated in the figure below.
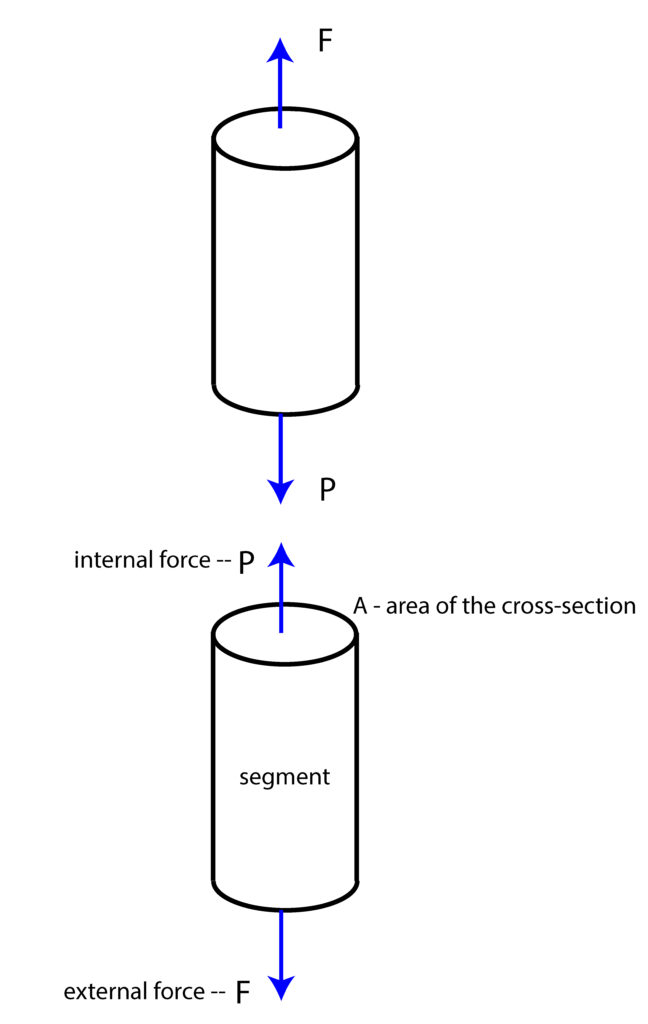
If the normal internal force is directed towards the cross-section, then stress is compressive, and otherwise, it is tensile.