Determine the Resultant of Two Forces Making Arbitrary Angles – Solved Problem – Fusion of Engineering, Control, Coding, Machine Learning, and Science

In this mechanics, physics, and statics tutorial, we explain how to find a resultant of two forces acting at a point. The two forces make arbitrary angles. We solve this problem by using three approaches. The first approach is based on applying the parallelogram method. The second approach is based on the triangle rule. The third approach is a numerical approach that is based on the application of the law of cosine and the law of sin. Every engineer and scientist need to known how to solve the problem explained in this tutorial. The YouTube video accompanying this tutorial is given below.

The problem is described below.

PROBLEM OF FINDING THE RESULTANT OF TWO FORCES

Two forces $F_{1}=30 [N]$ and $F_{2}=20 [N]$ (see the figure below). Determine their resultant (find the intensity of the resultant and angle).

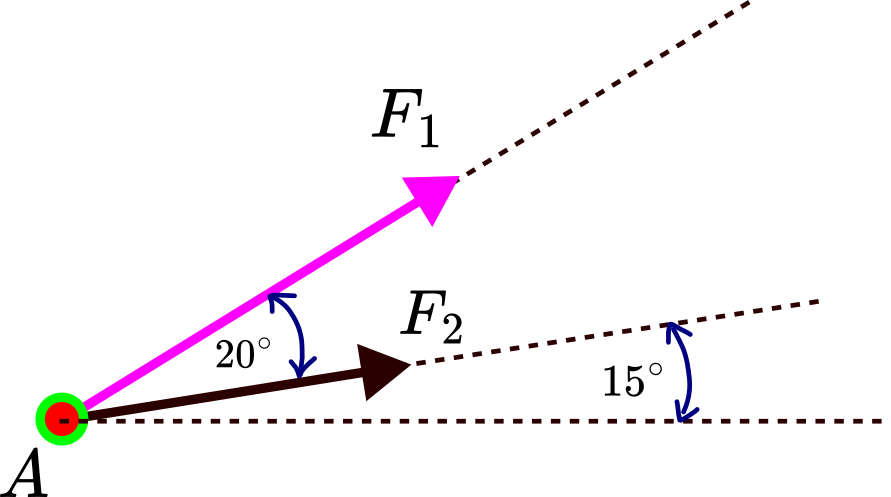
We will present three approaches to solve this problem.

Geometrical Solution Using the Parallelogram Method

We can use the parallelogram method. The parallelogram method is explained in the figure below.

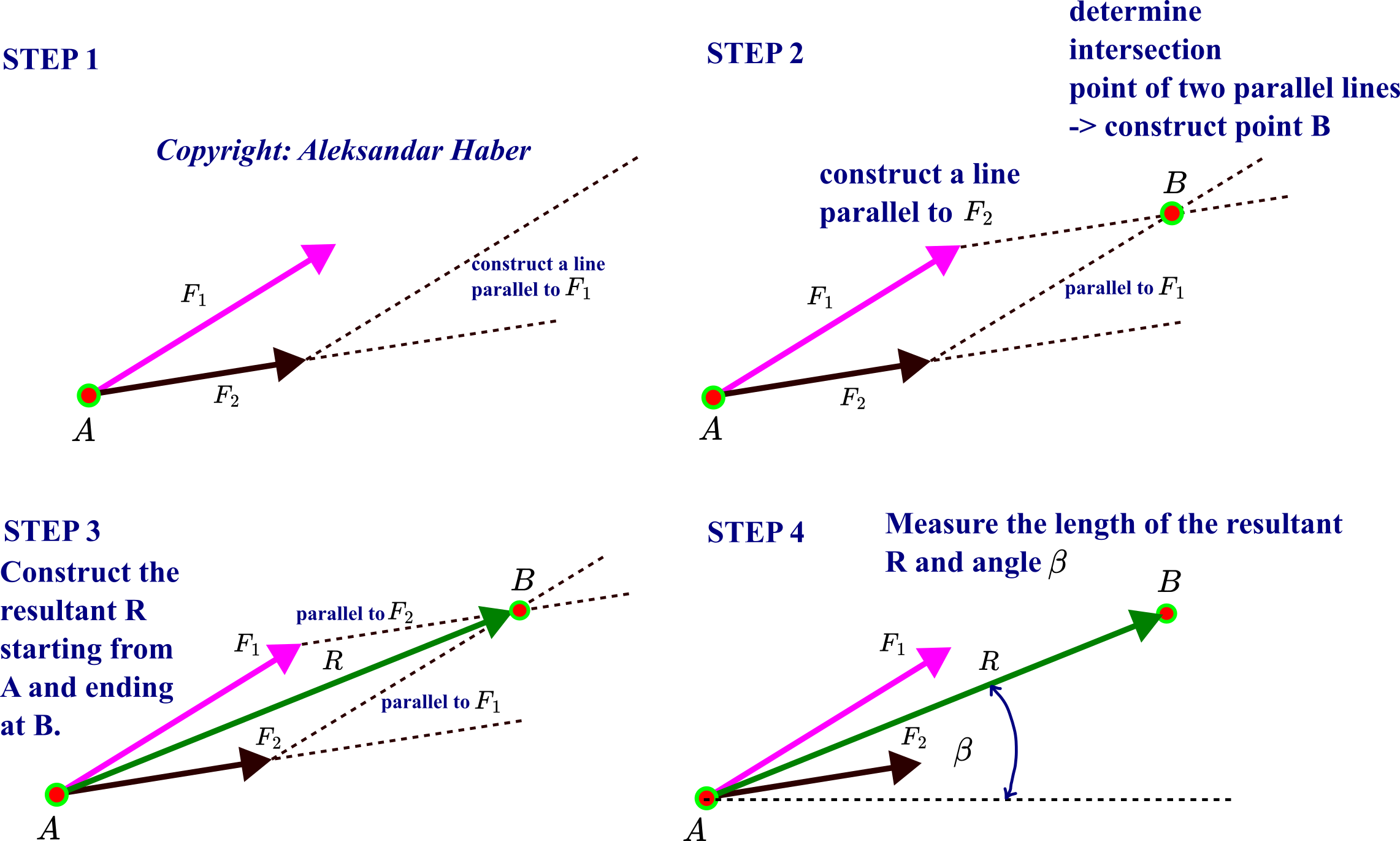
Figure 2: The parallelogram method for computing the resultant force.

To apply this method, you need a ruler measuring the distance and a protractor measuring the angle, or you can perform this task on a computer by using vector drawing software. This is a purely experimental graphical method. In step 1, we construct a line parallel to the action line of the force $F_{1}$ . In step 2, we construct a line parallel to the action line of the force $F_{2}$ , and find the intersection point of the two parallel lines. The intersection point is denoted by $B$ . In step 3, we construct the resultant $R$ starting from the point $A$ and ending at the point $B$ . In step 4, we measure the length of the resultant $R$ and the angle $\beta$ .

The length of the resultant force is $49.270997$ and the angle $\beta$ is $\beta=27.01972$ .

Geometrical Solution Using the Triangle Rule

The triangle rule for determining the resultant is similar to the parallelogram rule explained above. 1

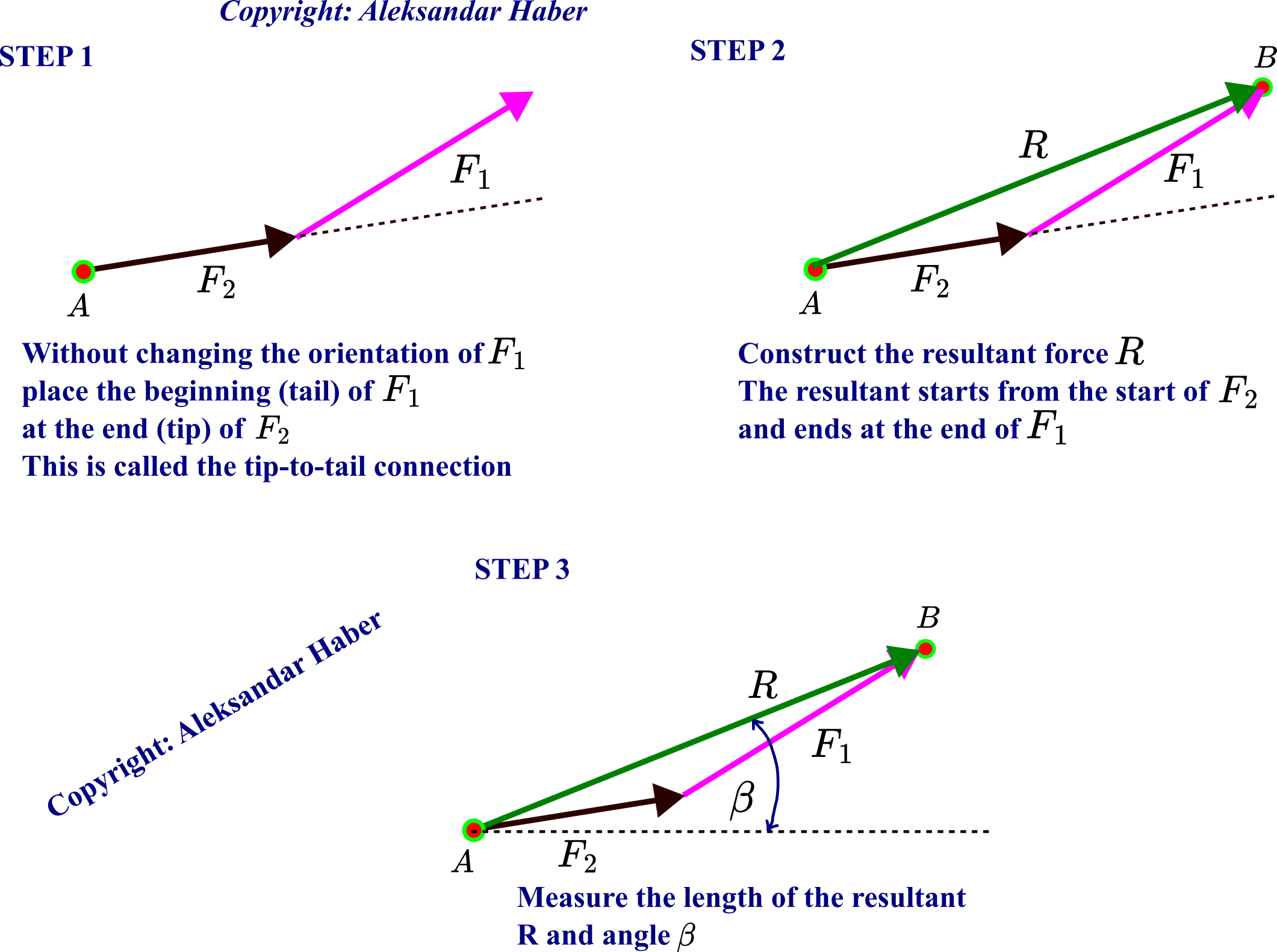
Figure 3: The triangle rule for computing the resultant.

In step 1, without changing the orientation of the force $F_{1}$ , we translate the force $F_{1}$ such that the beginning of the force $F_{1}$ is placed at the end of the force $F_{2}$ . That is, the tail of the force $F_{1}$ is placed at the tip of the force $F_{2}$ . This is called the “tip-to-tail” connection. In step 2, we connect the start (tail) of force $F_{2}$ to the end (tip) of force $F_{1}$ . In this way, we construct the resultant force $R$ . In step 3, we measure the length of the resultant $R$ and the angle $\beta$ .

The length of the resultant force is $49.270997$ and the angle $\beta$ is $\beta=27.01972$ .

Trigonometric Solution

To be able to solve this problem, we need to use the law of cosines and the law of sines. Consider a triangle shown below.

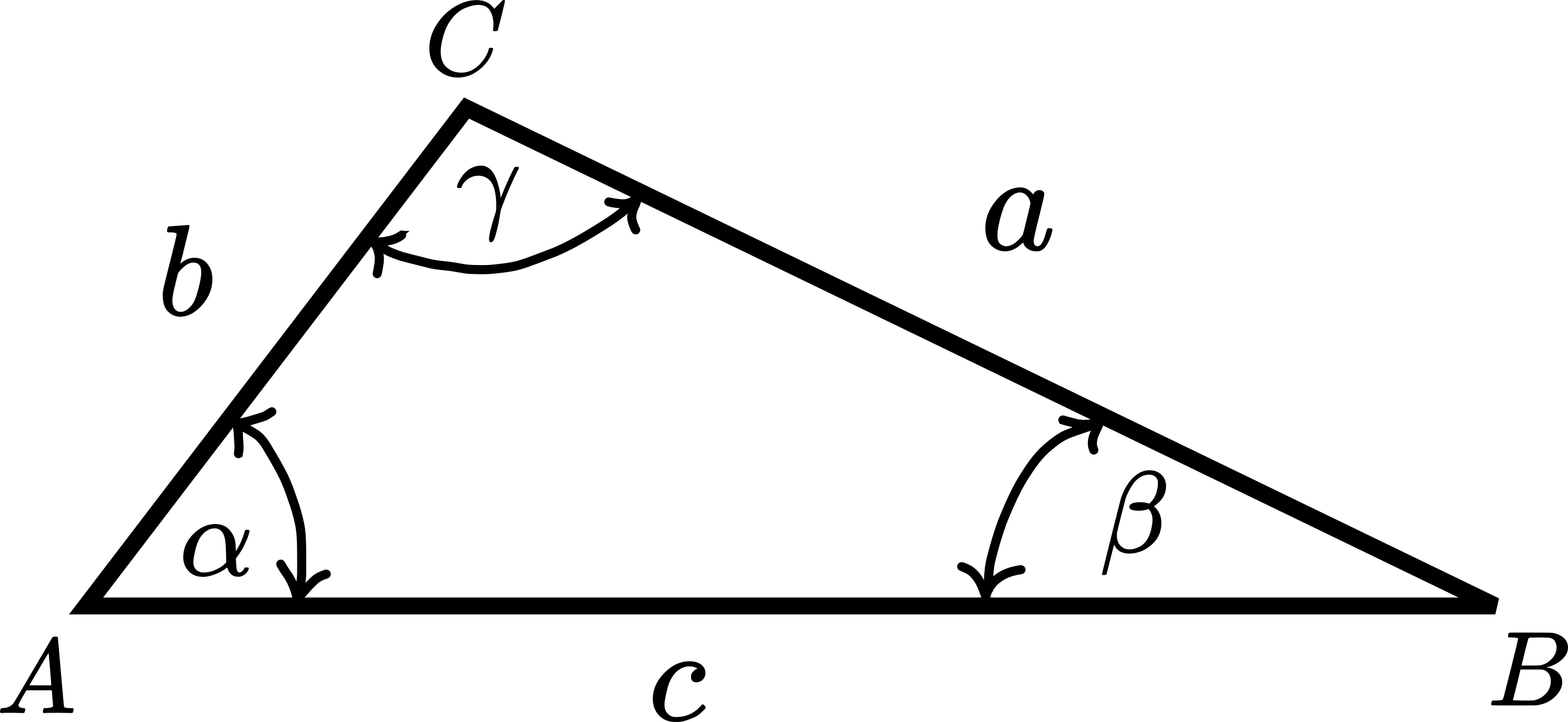
Figure 4: Triangle for explaining the cosines and sine laws.

The law of cosines states the following:

(1) $\begin{align*}c^{2}=a^{2}+b^{2}-2\cdot a\cdot b\cdot \cos(\gamma) \\a^{2}=b^{2}+c^{2}-2\cdot b\cdot c\cdot \cos(\alpha) \\b^{2}=a^{2}+c^{2}-2\cdot a\cdot c\cdot \cos(\beta) \end{align*}$

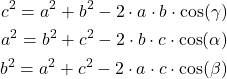
The law of sines states the following:

(2) $\begin{align*}\frac{a}{\sin (\alpha)}=\frac{b}{\sin (\beta)}=\frac{c}{\sin (\gamma)}\end{align*}$

After revising the laws of cosines and sines, let us go back to our problem. Consider the resultant force triangle shown in the figure below.

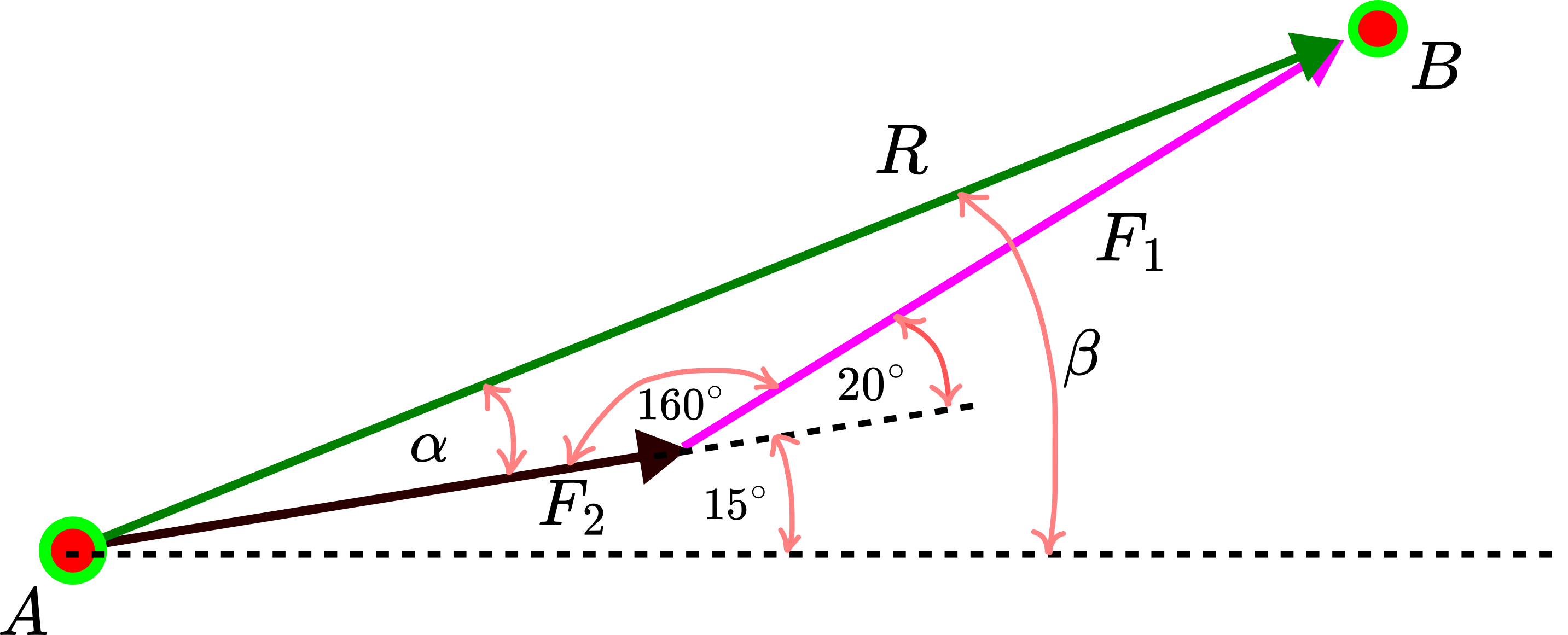
Fig. 5: Sketch for computing the resultant force angle and intensity by using trigonometry.

We want to compute the intensity of the resultant force $R$ and the angle $\beta$ . For that, we are going to use the law of cosines. By applying the law of cosines, we obtain

(3) $\begin{align*}|R|^{2}& =|F_{1}|^{2}+|F_{2}|^{2}-2|F_{1}||F_{2}|\cos (160^{\circ}) \\|R|^{2}& =|F_{1}|^{2}+|F_{2}|^{2}-2|F_{1}||F_{2}|\cos (180^{\circ}-20^{\circ}) \\|R|^{2}& =|F_{1}|^{2}+|F_{2}|^{2}+2|F_{1}||F_{2}|\cos (20^{\circ}) \end{align*}$

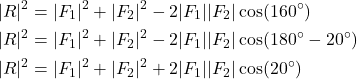
where $|R|$ , $|F_{1}|$ , and $|F_{2}|$ are the intensities of $R$ , $F_{1}$ , and $F_{2}$ forces. From the last equation, we obtain

(4) $\begin{align*}|R|& =\sqrt{|F_{1}|^{2}+|F_{2}|^{2}+2|F_{1}||F_{2}|\cos (20^{\circ}) }\end{align*}$

By inserting the values in a calculator or in a Python code (the code is given at the end), we obtain

(5) $\begin{align*}|R|=49.270997\end{align*}$

Here, it is important to keep in mind that while computing the intensity of the resultant force, we need to convert angles from degrees to radians since the cos function argument is expressed in radians in MATLAB and Python.

On the other hand, we compute the angle $\beta$ by computing the angle $\alpha$ . We compute the angle $\alpha$ by using the law of sines. Namely, from Fig. 5, we have

(6) $\begin{align*}\frac{|F_{1}|}{\sin (\alpha)}= \frac{|R|}{\sin (160^{\circ})}\end{align*}$

From the last equation, we have

(7) $\begin{align*}\sin (\alpha)= \frac{|F_{1}|}{|R|}\sin (160^{\circ})\end{align*}$

Finally, we obtain

(8) $\begin{align*}\alpha = \arcsin( \frac{|F_{1}|}{|R|}\sin (160^{\circ}) ) \end{align*}$

By substituting the values for $|F_{1}|$ and $|R|$ , we obtain

(9) $\begin{align*}\alpha=12.0197\end{align*}$

Finally, the angle $\beta$ is

(10) $\begin{align*}\beta=15+12.0197=27.01972\end{align*}$

The Python code for computing the resultant force is given below.

import numpy as np

F1=30
F2=20

# angles in degrees

a1=20
a2=15


# convert to radians

a1rad= a1*(2*np.pi)/360
a2rad= a2*(2*np.pi)/360

R=np.sqrt(F1**2+F2**2+2*F1*F2*np.cos(a1rad))

# test, using the original angle equal to 160
Rtest= np.sqrt(F1**2+F2**2-2*F1*F2*np.cos((180-a1)*(2*np.pi)/360))


# compute the angle 

angleAlphaRad=np.arcsin((F1/R)*np.sin((180-a1)*(2*np.pi)/360))

angleAlpha=angleAlphaRad*360/(2*np.pi)

betaAngle=angleAlpha+a2

PROBLEM OF FINDING THE RESULTANT OF TWO FORCES

Geometrical Solution Using the Parallelogram Method

Geometrical Solution Using the Triangle Rule

Trigonometric Solution

admin

You might also like

2. Introduction to Pandas structures: Series and DataFrame structures

Introduction to the Concept of Stress – Normal Stress

Introduction to Feedback Linearization