In this mathematics, calculus, and trigonometry tutorial, we provide clear and concise explanation of the law of sines. The law of sines is a very important trigonometric law that is often used in mechanical and electrical engineering, as well as in robotics and physics. The YouTube video accompanying this tutorial is given below.
Basic Definitions
- An acute angle is an angle that is larger than 0 degrees and less than 90 degrees.
- An obtuse angle is an angle that is larger than 90 degrees and less than 180 degrees.
- A triangle is called right (right triangle) if two sides are perpendicular. That is, a right triangle has two sides that are creating an angle of 90 degrees. An angle of 90 degrees is called the right angle.
- A triangle is called oblique (oblique triangle) if none of its angles is a right angle. The figure below shows two examples of oblique triangles.
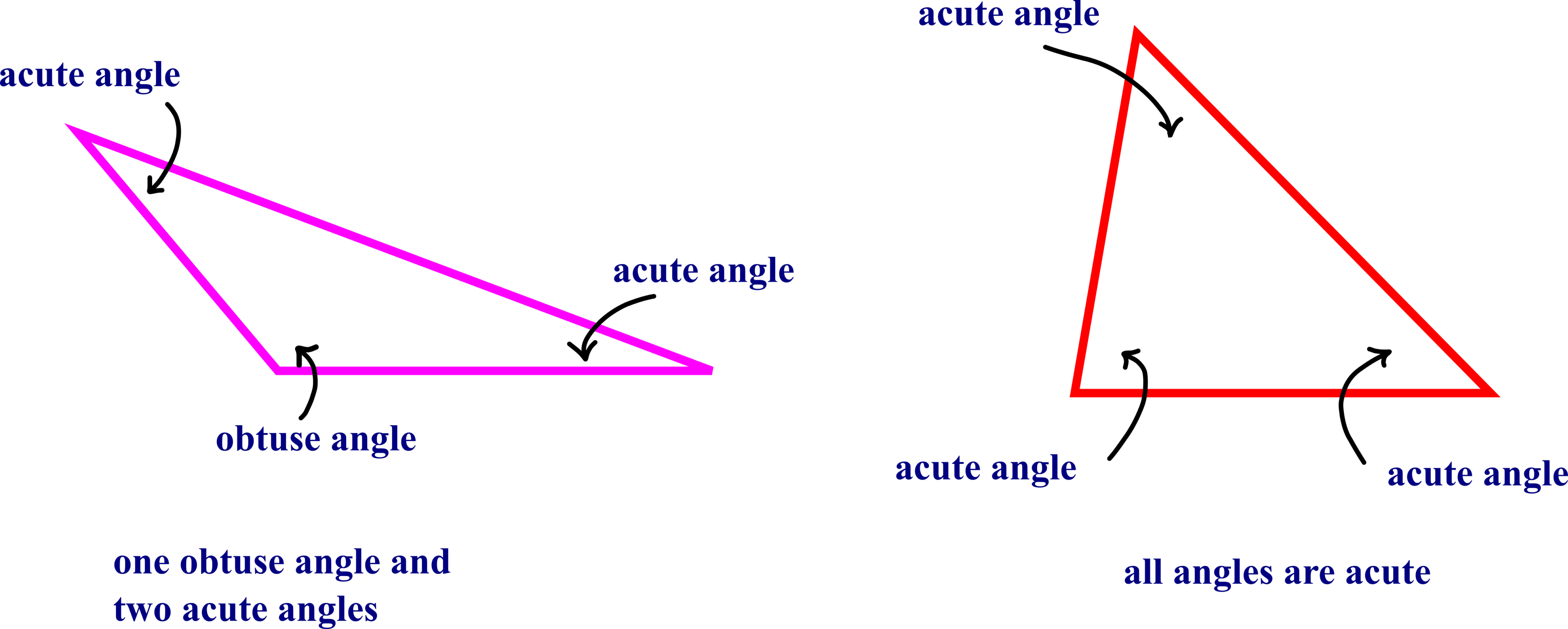
What does it mean to solve a triangle? To solve a triangle means to determine the numerical values of its sides and angles.
Solving a right triangle
Consider a right triangle shown in the figure below.
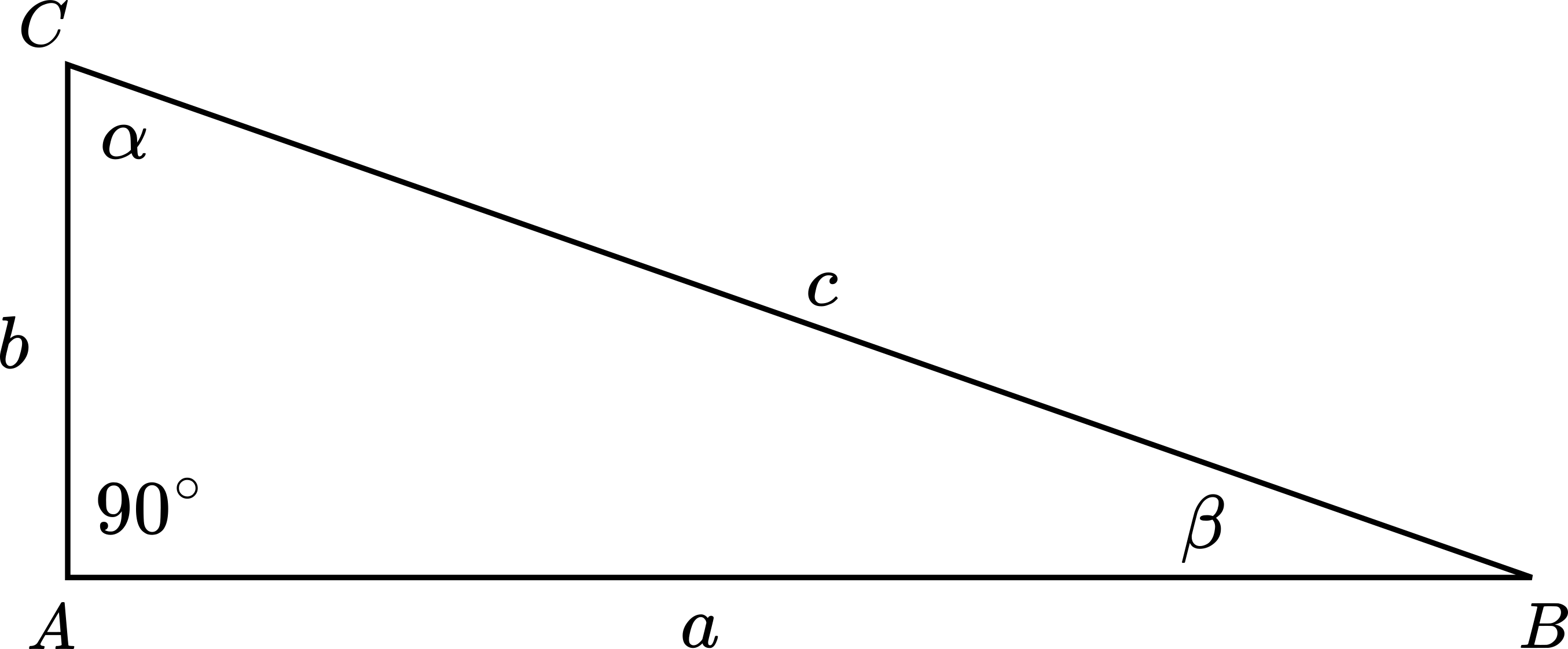
Figure 2: Right triangle.
To solve the right triangle shown in the figure above we need to know either
- (a) One of the acute angles (
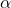 or
or 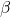 ) and one of the sides.
) and one of the sides. - (b) Two sides. In this case, we can use the Pythagorean theorem to calculate the third side, and basic trigonometry to compute other angles.
Case (a): Solve the right triangle if an acute angle and one of the sides are known.
Let us assume that the angle ![]() is known and the side
is known and the side ![]() is known. Our task is to compute the sides
is known. Our task is to compute the sides ![]() and
and ![]() and the angle
and the angle ![]() . We have
. We have
(1) ![]()
Then, we have
(2) ![]()
Case (b): Solve the right triangle if two sides are known
Without the loss of generality, let us assume that ![]() and
and ![]() are known. Then, by using the Pythagorean theorem, we have
are known. Then, by using the Pythagorean theorem, we have
(3) 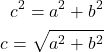
The angle ![]() can be determined as
can be determined as
(4) 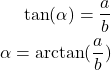
Solve Oblique Triangles – Use the Law of Sines
The next question is how to solve oblique triangles. Depending on the case and what is given, we either need to use the law of sines or the law of cosines. The law of sines will be covered in this lecture, and the law of cosines will be covered in the next lecture.
First, let us briefly state the law of sines. Consider the oblique triangle shown in the figure below.
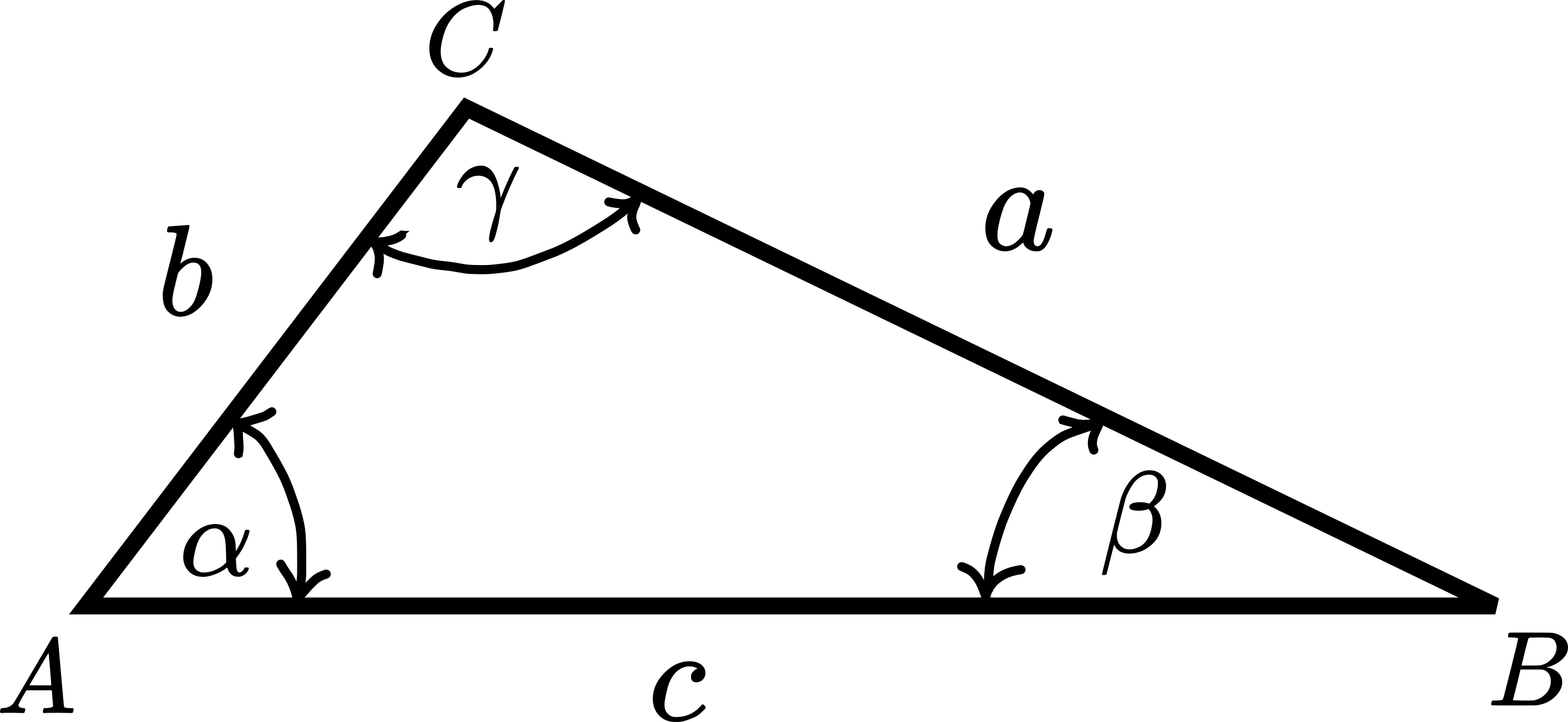
The law of sines can be mathematically expressed as
(5) ![]()
We use the law of sines to solve oblique triangles when
- Two angles and a side are known.
- Two sides are known and one angle that is not enclosed by these sides is known. In this case, under certain scenarios, it might happen that the triangle is not uniquely determined and there might be two solutions for the corresponding angle. If this happens, this case is called the ambiguous case.
Solve a Triangle Using the Law of Sines – Example 1
Problem: This example explains how to solve a triangle when two angles and a side are given. Given ![]() ,
, ![]() , and
, and ![]() , solve the triangle shown in the figure below.
, solve the triangle shown in the figure below.
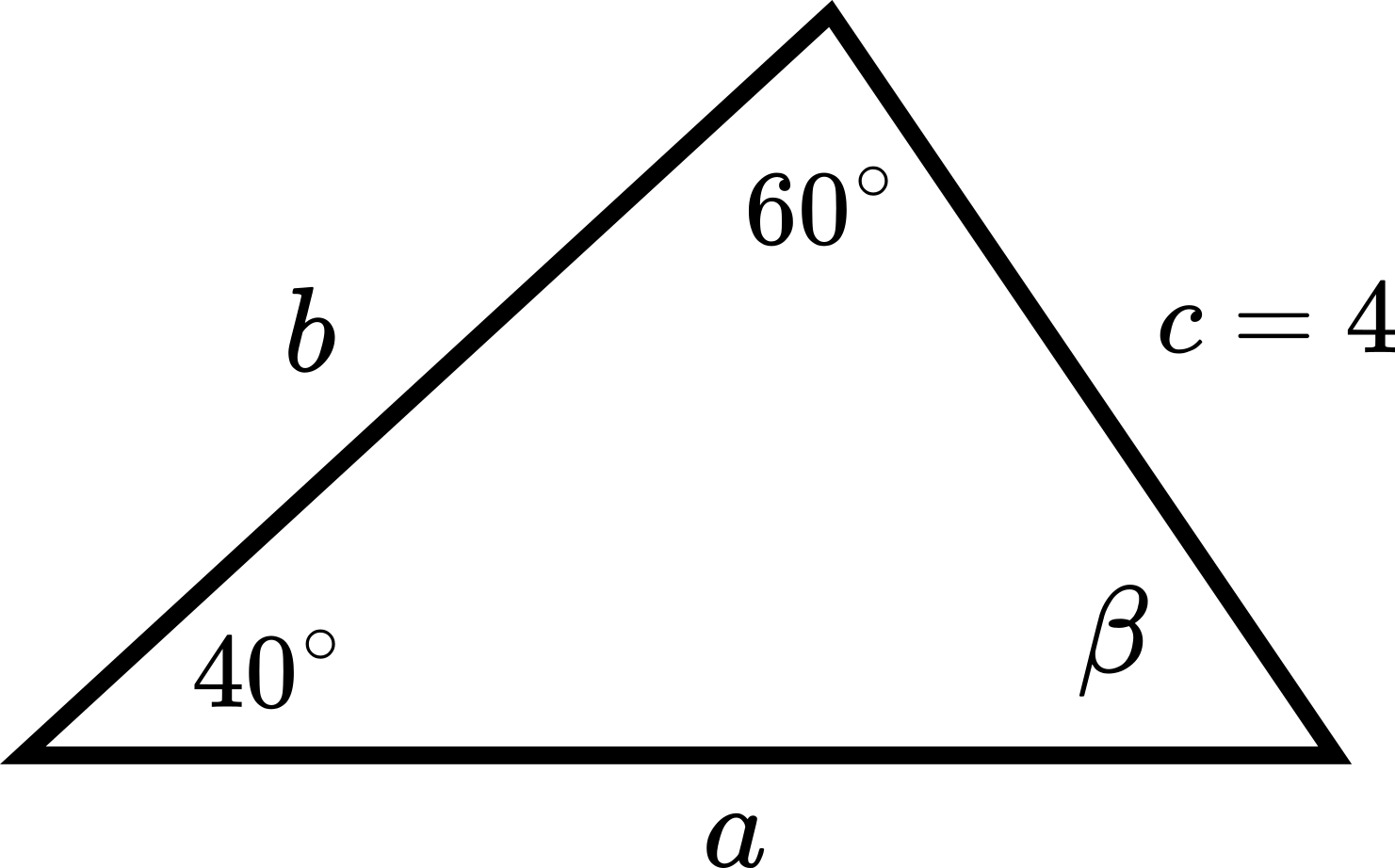
Solution: By applying the law of sines, we have
(6) ![]()
The angle ![]() can be determined as follows
can be determined as follows
(7) 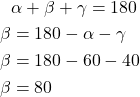
By substituting the values in (6), we obtain
(8) ![]()
From the last equation, we obtain
(9) 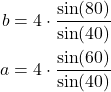
By converting angles to radians and by calculating the values, we obtain (the Python code is given below)
(10) 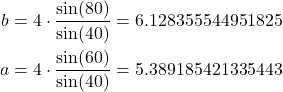
The Python code for computing the solution is given below.
import numpy as np
c=4
alpha= 60 * (2*np.pi/360)
beta= 80 * (2*np.pi/360)
gamma= 40 * (2*np.pi/360)
a= c*np.sin(alpha)/np.sin(gamma)
b= c*np.sin(beta)/np.sin(gamma)Solve a Triangle Using the Law of Sines – Example 2
This example explains how to solve a triangle when two sides and an angle are given. Given ![]() ,
, ![]() , and
, and ![]() solve the triangle shown in the figure below.
solve the triangle shown in the figure below.
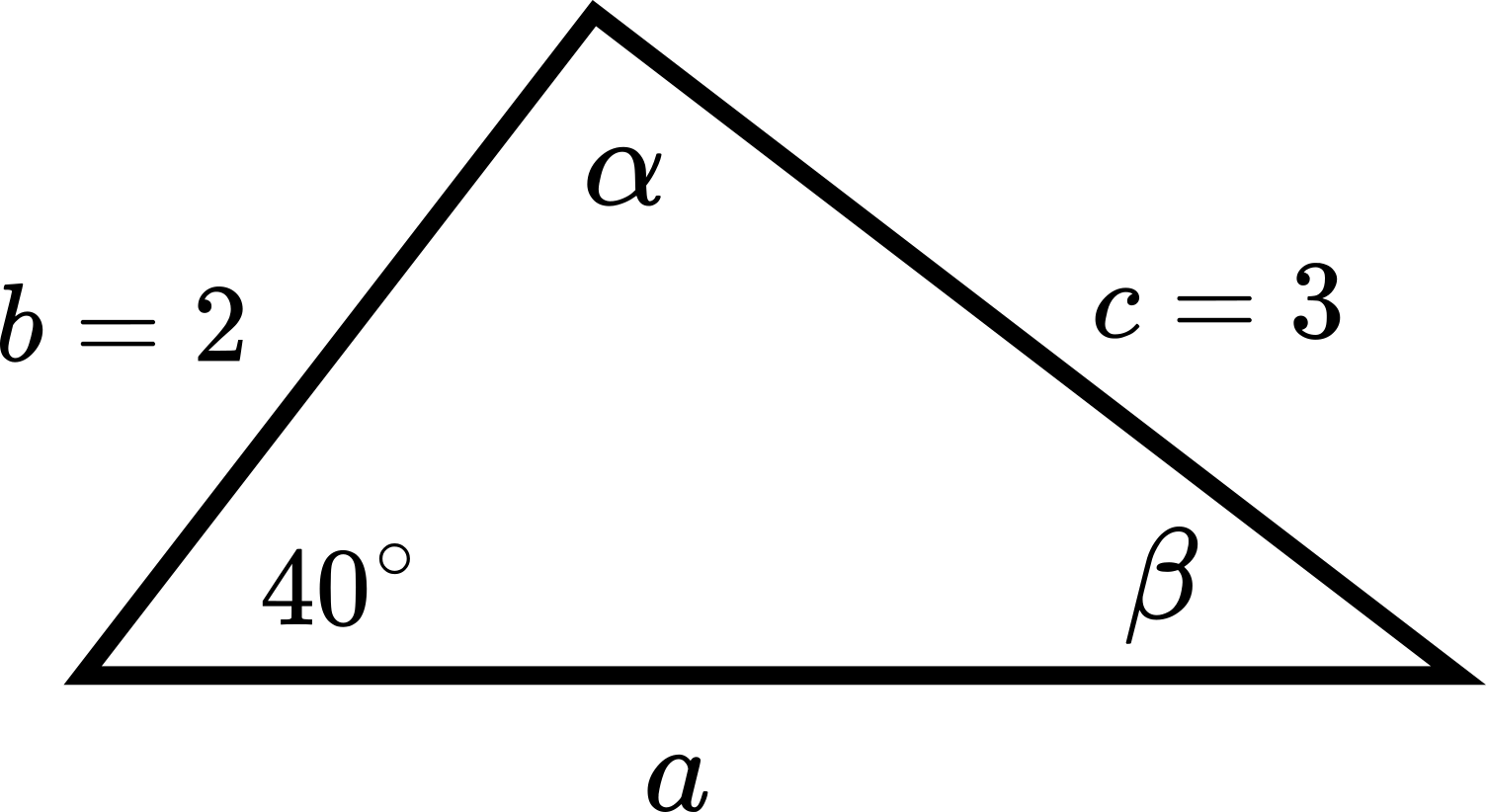
Solution: By applying the law of sines, we have
(11) ![]()
By substituting the values, we obtain
(12) ![]()
By substituting the given values in the last equation, we obtain
(13) ![]()
From the last equation, it follows that
(14) 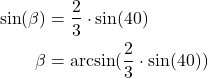
The angle ![]() in radians and degrees is
in radians and degrees is
(15) ![]()
The angle ![]() is then determined by
is then determined by
(16) 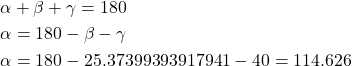
By using this value and (13), we obtain
(17) 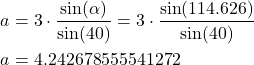
The Python code for solving this problem is given below
import numpy as np
b=2
c=3
gamma= 40 * (2*np.pi/360)
beta = np.arcsin((2/3)*np.sin(gamma))
betaDeg= beta* 360/(2*np.pi)
alphaDeg = 180 -betaDeg- 40
alpha= alphaDeg * (2*np.pi/360)
a = c* np.sin(alpha)/np.sin(gamma)