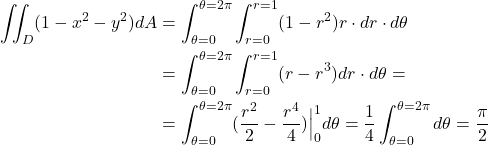In this mathematics and calculus tutorial, we explain how to solve double integrals by using polar coordinates. The YouTube tutorial is given below.
The problem of Solving Double Integrals
Calculate the value of the double integral
(1) ![]()
where the domain of integration
Solve Double Integrals by Using Polar Coordinates
To solve this integral, we introduce the polar coordinates
(2) ![]()
The integration domain ![]() is a circle with the radius of
is a circle with the radius of ![]() . The equation of the circle boundary in the Cartesian coordinates is
. The equation of the circle boundary in the Cartesian coordinates is
(3) ![]()
The inside of the circle is described by the following inequality
(4) ![]()
Consequently, in the Cartesian coordinates, the integration domain ![]() is
is
(5) ![]()
By substituting the polar coordinates (6) in
(6) ![]()
We obtain
(7) 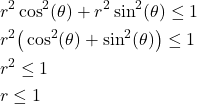
The angle ![]() is in the interval from
is in the interval from ![]() to
to ![]() since we need to describe the complete circle. Consequently, the integration domain in the polar coordinates takes the following form
since we need to describe the complete circle. Consequently, the integration domain in the polar coordinates takes the following form
(8) ![]()
On the other hand, the term ![]() in the original integral (1) can be expressed as follows in the polar coordinates
in the original integral (1) can be expressed as follows in the polar coordinates
(9) ![]()
By substituting (6) and (9) in the original integral (1) and by taking into account the integration domain in the polar form (8), the original integral becomes:
(10)