- Transform units:
a)![Rendered by QuickLaTeX.com 5 [\frac{miles}{hour}]](https://aleksandarhaber.com/wp-content/ql-cache/quicklatex.com-d414b179b6f0251363edef610f99a31f_l3.png) to
to ![Rendered by QuickLaTeX.com [\frac{kilometer}{second}]](https://aleksandarhaber.com/wp-content/ql-cache/quicklatex.com-54336898f5622c3d788da4d507b547a4_l3.png)
b)![Rendered by QuickLaTeX.com 120 [\frac{centimeter}{second}]](https://aleksandarhaber.com/wp-content/ql-cache/quicklatex.com-b75c9a40df308aeae41324b50c02a237_l3.png) to
to ![Rendered by QuickLaTeX.com [\frac{milimeter}{hour}]](https://aleksandarhaber.com/wp-content/ql-cache/quicklatex.com-dd11fac344e39836bdd376dcb93631f3_l3.png)
c)![Rendered by QuickLaTeX.com 10^{6} [\frac{meter}{second}]](https://aleksandarhaber.com/wp-content/ql-cache/quicklatex.com-d647668321d36ddde5636d95f24d2b36_l3.png) to
to 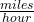
2. Interest rates. Initially, you borrowed ![]() from a bank. The yearly interest rate is
from a bank. The yearly interest rate is ![]() . The loan is for
. The loan is for ![]() years. After
years. After ![]() years, how much money do you have to return to the bank?
years, how much money do you have to return to the bank?
3. Simplify expression:
(1) ![]()
4. Find
(2) 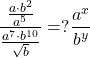
5. Sketch the functions:
(3) 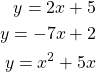
6. Solve the quadratic equations
(4) 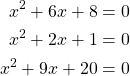
7. Simplify the fractions:
(5) ![]()
8. Two cars are approaching each other. The velocity of the first car is
9. A police car is chasing a criminal in another car. The velocity of the police car is ![]() and the velocity of the criminal’s car is
and the velocity of the criminal’s car is ![]() . Both cars are moving in the same direction along the straight line (the criminal is trying to escape ). If the initial distance between the cars was
. Both cars are moving in the same direction along the straight line (the criminal is trying to escape ). If the initial distance between the cars was ![]() , compute the time it takes for the police car to reach the criminal’s car.
, compute the time it takes for the police car to reach the criminal’s car.
10. State the definition and graphically explain Newton’s third law.
11. An object is moving along a straight line. Its position that is a function of time is given by the following table.
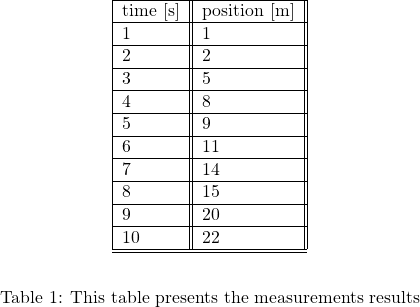
Estimate
a) Velocity at the time instant ![]()
b) Velocity at the time instant ![]()
c) Acceleration at the time instant ![]()
12. Given two functions:
(6) ![]()
a) Sketch these functions on a single graph
b) Numerically compute their intersection points
13. What is a free body diagram?
14. a) Sketch the following vectors
(7) ![]()
b) Calculate the magnitudes of these vectors and calculate their angles with respect to the positive x-direction.
15. If the length of the vector is ![]() and if its angle with respect to the positive
and if its angle with respect to the positive ![]() direction is
direction is ![]() degrees, compute the
degrees, compute the ![]() and
and ![]() projections of this vector.
projections of this vector.
16. In the following figure (a)-d) panels), the vectors are defined with their magnitudes and angles. Calculate ![]() and
and ![]() projections of these vectors.
projections of these vectors.
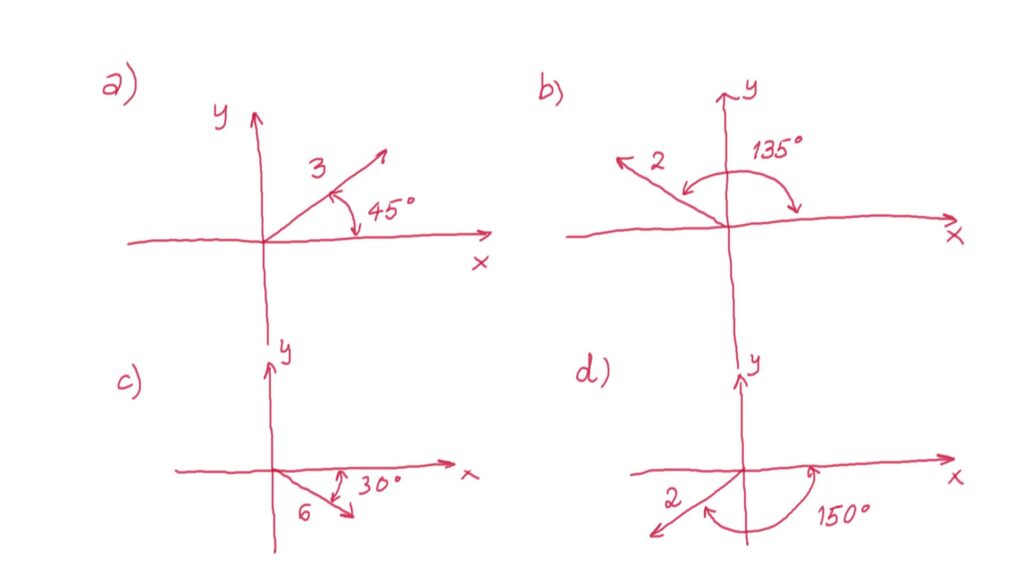
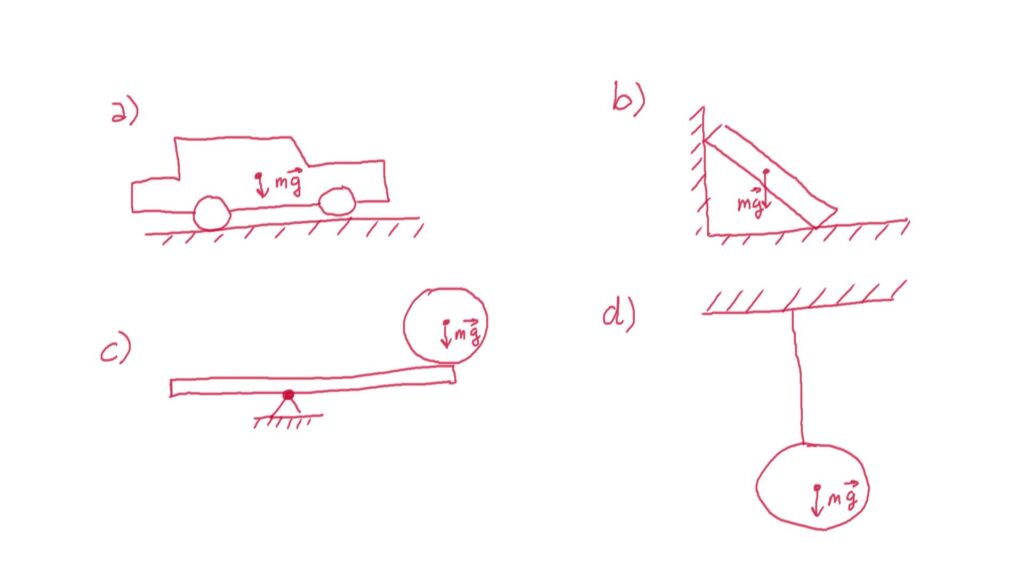
17. Sketch free body diagrams of the objects sketches in figures below
a) free body diagram of the car
b) free body diagram of the bar
c) free body diagram of the ball and the bar
d) free body diagram of the ball and the hanging cord
18. What is a moment of a force?
19. Given the force ![]() , angle, and distance
, angle, and distance ![]() , compute the moment of the force
, compute the moment of the force ![]() with respect to the point A for the cases given in the panels of the figure below.
with respect to the point A for the cases given in the panels of the figure below.
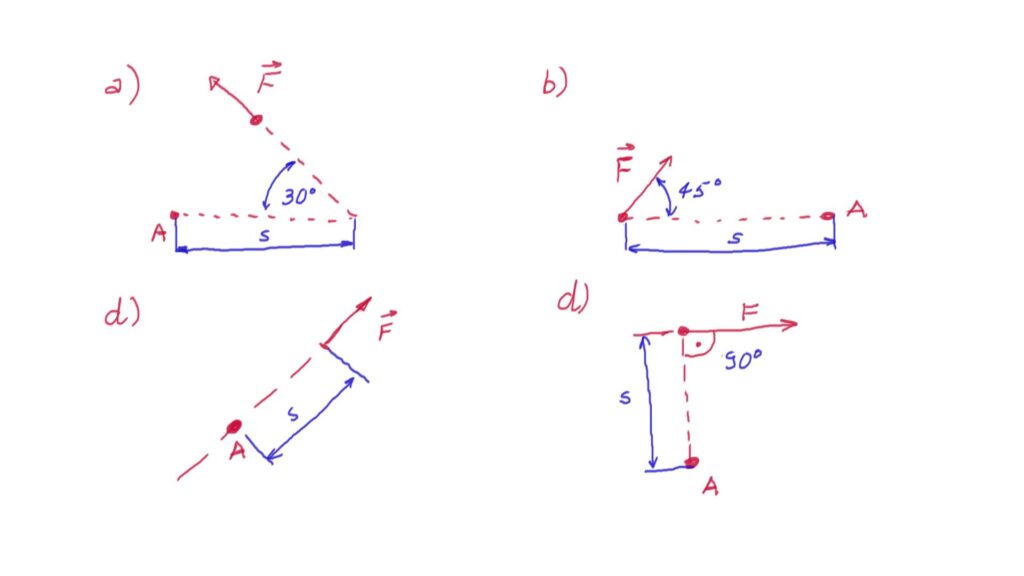
20. What is a mechanical advantage? Give an example.
21. Explain Newton’s third law. Give a graphical as well as text explanation.
22. Explain a friction force. Give a graphical as well as text explanation.
23. What is a difference between object’s mass and object’s weight?
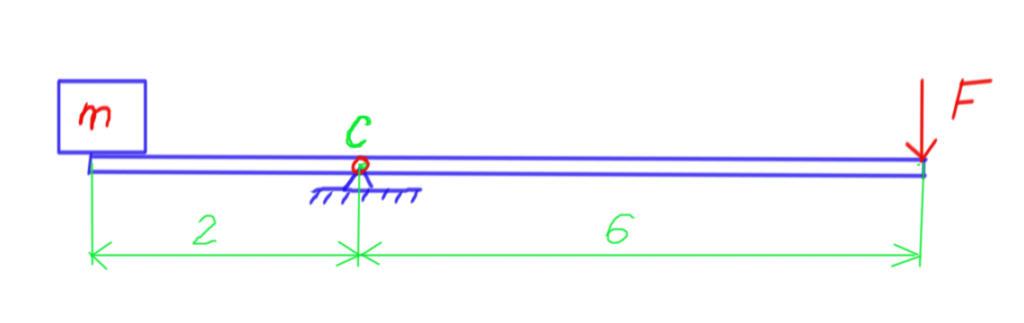
24. Consider a lever mechanism shown in the figure below. A box of the mass m=100 kg is being supported by one side of the lever.
a) Sketch free body diagrams of the box and the lever.
b) Calculate the magnitude of the force ![]() that needs to be applied to the lever, such that the lever mechanism is at rest at the horizontal position.
that needs to be applied to the lever, such that the lever mechanism is at rest at the horizontal position.
c) What is the mechanical advantage of the lever?
25. Solve the system of linear equations for ![]()
(8) 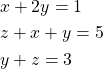
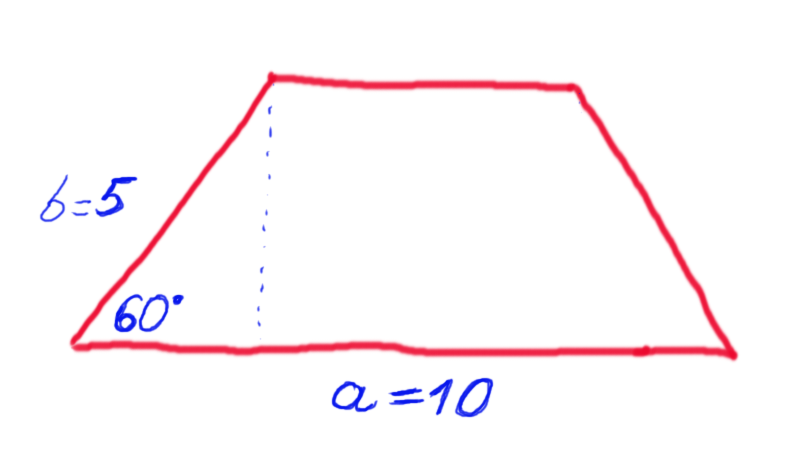
26. See the figure below. The base length of the trapezoid is 10. The angle is 60 degrees and the length of the inclined side is 5. Compute the area of the trapezoid?
27. How many liters of water can a cylindrical barrel hold if the base of the barrel has a diameter of ![]() [m] and the height of
[m] and the height of ![]() ?
?
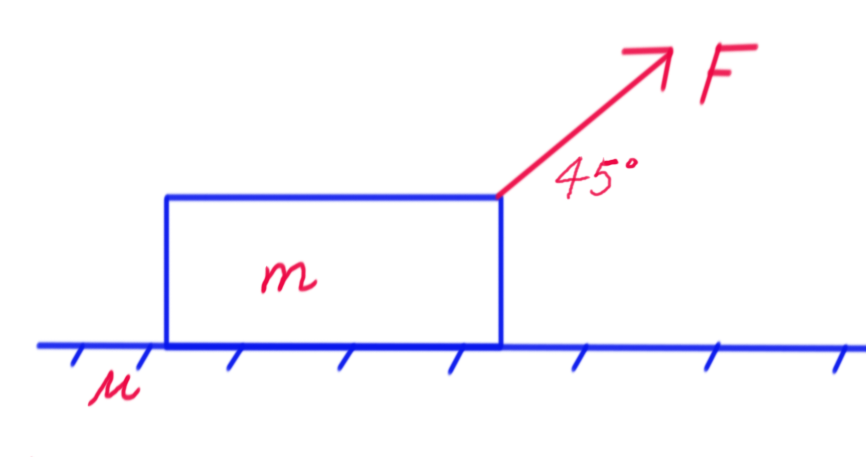
28. A force ![]() is acting on a box of the mass
is acting on a box of the mass ![]() (see the figure below). The coefficient of friction between the surface and the box is
(see the figure below). The coefficient of friction between the surface and the box is ![]() .
.
a) Sketch a free body diagram of the box?
b) What is the maximal intensity of the force ![]() that can be applied to the box such that the box remains still (at rest)?
that can be applied to the box such that the box remains still (at rest)?
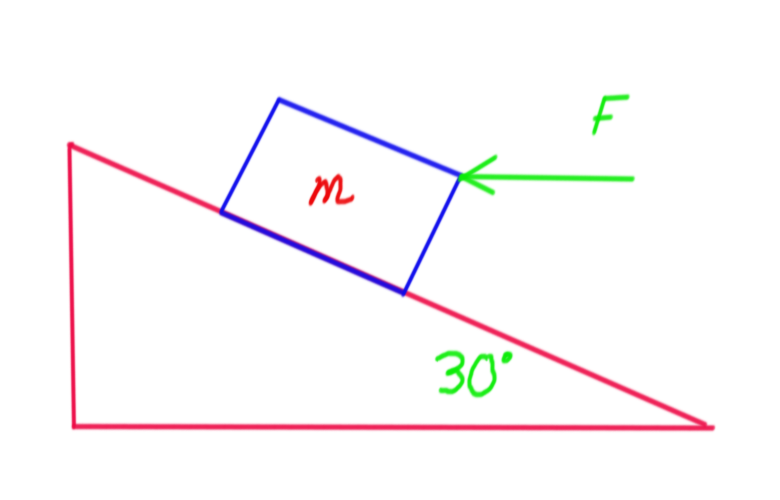
29. A force ![]() is acting on a box of the mass
is acting on a box of the mass ![]() on an inclined plane with an angle of
on an inclined plane with an angle of ![]() degrees. The inclined plane is without friction (no friction force).
degrees. The inclined plane is without friction (no friction force).
a) Sketch a free body diagram of the box.
b) What is the force ![]() (the force is horizontal) that needs to be applied to the box such that the box does not move.
(the force is horizontal) that needs to be applied to the box such that the box does not move.
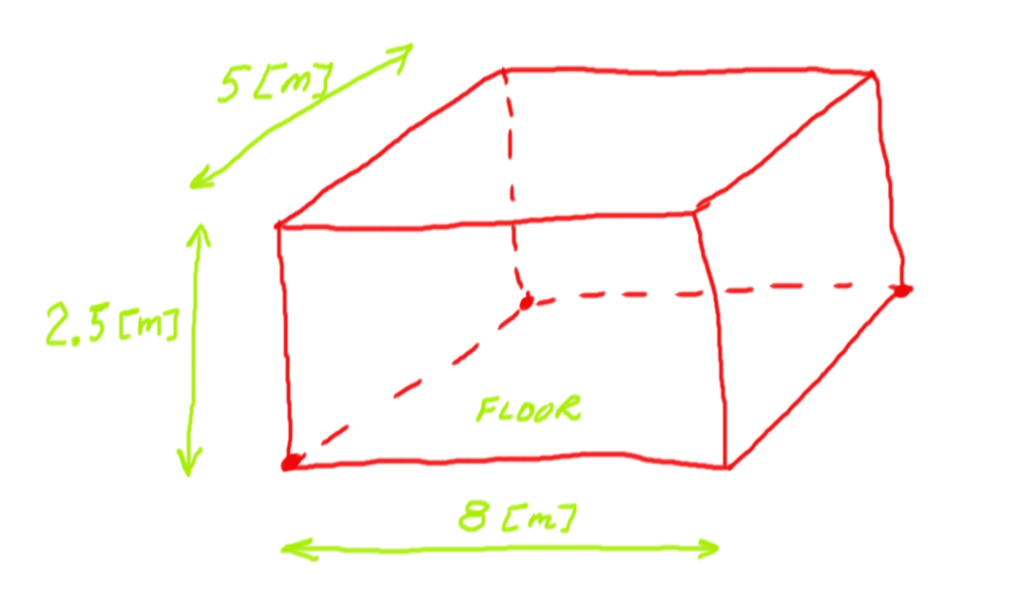
31. You are paining a room (see the figure below). The room dimensions are ![]() . You are painting all the inner walls of the room except the floor. You are also painting a ceiling. With a single container of paint, you are able to paint
. You are painting all the inner walls of the room except the floor. You are also painting a ceiling. With a single container of paint, you are able to paint ![]() (1.5 square meters). How many containers of paint do you need to purchase to paint the room (everything except the floor)?
(1.5 square meters). How many containers of paint do you need to purchase to paint the room (everything except the floor)?