In this algebra and calculus tutorial, we will learn how to divide complex numbers. That is, we will learn how to compute a quotient of two complex numbers. Division of complex numbers is very important for electrical and mechanical engineering students who are interested in control theory, signal processing, robotics, electrical networks, power systems, etc. We will also learn how to verify the analytical computations in Python. The YouTube tutorial accompanying this post is given below.
Division of Complex Number: Problem and Solution
We are given an expression involving two complex numbers
(1) ![]()
where ![]() is the imaginary unit. We want to provide answers to the following questions and problems:
is the imaginary unit. We want to provide answers to the following questions and problems:
- Is this expression a complex number?
- If yes, then express this complex number in the standard (rectangular) form:
(2)
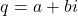
where is the real part and
is the real part and 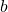 is the imaginary part of the complex number
is the imaginary part of the complex number 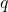 .
.
The answer to the first question is YES. This will become clear once we solve the second problem. More generally, the quotient of two complex numbers is a complex number.
Let us now address the second problem. The problem will be solved by using two steps. Our goal is to compute the real and imaginary parts of the complex number ![]() . The issue is with the complex number
. The issue is with the complex number ![]() in the denominator of the number
in the denominator of the number ![]() . This complex number prevents us from expressing
. This complex number prevents us from expressing ![]() as the sum of real and imaginary parts. To get rid of this complex number in the denominator, let us first observe the following. Let
as the sum of real and imaginary parts. To get rid of this complex number in the denominator, let us first observe the following. Let ![]() be a complex number with the real part
be a complex number with the real part ![]() and the imaginary part
and the imaginary part ![]() . Then, let us multiply the complex number
. Then, let us multiply the complex number ![]() with its complex conjugate
with its complex conjugate ![]()
(3) ![]()
The last expression can be written as follows
(4) ![]()
This example shows us that by multiplying a complex number with its conjugate we actually obtain a real number. Also, it is important to observe that the (3) expression is very similar to the classical expression for the difference of two squares:
(5) ![]()
For example,
(6) ![]()
We can use this simple observation to rationalize the complex quotient (1). This leads us to step 1 of solving this problem:
STEP 1: Multiply the numerator and the denominator of the complex quotient expression by the complex conjugate of the complex number in the denominator.
Let us follow this step. As a result, we have
(7) ![]()
where ![]() is the complex conjugate of the complex number
is the complex conjugate of the complex number ![]() that is in the denominator of the original expression. The idea here is to get rid of the complex number in the denominator of the original quotient expression. As explained previously, we can do that by multiplying a complex number with its complex conjugate.
that is in the denominator of the original expression. The idea here is to get rid of the complex number in the denominator of the original quotient expression. As explained previously, we can do that by multiplying a complex number with its complex conjugate.
STEP 2: Determine the real and imaginary part of the expression from STEP 1:
Let us perform this step. From (7), we have
(8) 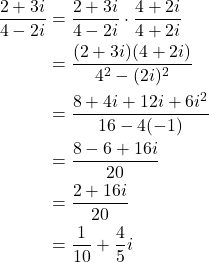
This solves the problem. The real part is ![]() and the imaginary part is
and the imaginary part is ![]() .
.
Python Script for Dividing Complex Numbers
In the sequel, we present the Python script that can be used to verify these results. There are two approaches. The first approach is to use the built-in Python complex number algebra. The second approach is to use the Python symbolic computation library SymPy. The Python script is given below.
# -*- coding: utf-8 -*-
"""
Division of Complex Numbers
@author: Aleksandar Haber
Date: November 2023
"""
# two approached for dividing complex numbers in
# Python
# First approach - by using the built-in comple operations
# 1j is the standard notatio for the imaginary unit in Python
R1=(2+3j)/(4-2j)
# Second approach - by using SymPy
# - symbolic Python library
from sympy import *
init_printing()
# I is the imaginary unit in SymPy
z1 = 2 + I*3
z2 = 4 - I*2
R2=z1/z2
R3=simplify(R2)
R3
print(R3)