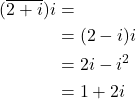In this tutorial, we provide an easy-to-understand introduction to complex numbers. This tutorial is specially designed for high school and engineering students. This is the first tutorial on complex numbers. In this tutorial, we will
- Motivate the need for complex numbers.
- Explain what is an imaginary unit.
- State the definition of complex numbers
- Provide a graphical interpretation of complex numbers
- Explain how to perform basic operations on complex numbers (sum, difference, and product)
- Define a conjugate of a complex number
In the second tutorial, we will the polar form of complex numbers, modulus of complex numbers, and the argument of complex numbers. This tutorial series is very important for mechanical and electrical engineers who are interested in dynamical systems, signal processing, electrical networks, and control engineering. A proper understanding of complex numbers is very important for a proper understanding of dynamical systems, fluid dynamics, electrical networks, control engineering, and signal processing.
The YouTube video accompanying this tutorial is given below.
Motivation for Introducing Complex Numbers
Complex numbers are actually not complex to understand. In fact, they are relatively easy to understand, so you should not be afraid of the word complex in the expression “complex number”.
First, let us try to solve this quadratic equation:
(1) ![]()
We want to provide answers to the following questions
- How many solutions does this equation have?
- What are the solutions?
This is a relatively simple equation. Since it is a quadratic equation, this equation should have two solutions. The solutions are computed as follows
(2) ![]()
Now, let us slightly modify this equation by changing a sign, and you will immediately notice a big difference
(3) ![]()
Now, again, we want to provide the answers to the following questions
- How many solutions does this equation have?
- What are the solutions?
Well, since this is a quadratic equation, we should have two solutions. This is correct. We should obtain two solutions. But, wait a second, can we actually solve this equation by using the knowledge of algebra we learned in basic courses? Let us try to do that
(4) ![]()
From here, we do not know how to proceed. Does it look confusing? How can a square of a number be equal to -1? Is this completely illogical? Mathematicians have been struggling with this problem for centuries, and today we do not even recognize that this is a problem. However, in fact, it is. At first glance, to our human mind, it looks like the last equation does not make sense.
Definition of Imaginary Unit and Complex Numbers
The issue described in the previous section comes from the main properties of the real numbers. One of the important properties of real numbers is that their squares are positive numbers. That is, if we take a real number and, if we compute its square, the result cannot be negative. So, the answer to our question can be that the equation (3) does not have a solution in the set of real numbers! This is a completely legitimate answer. However, this equation actually has the solution, but not in the set of real numbers. It has a solution that belongs to the set of complex numbers. The set of complex numbers is denoted by ![]() .
.
Before we formally define the complex numbers, we first need to introduce the concept of imaginary unit ![]() :
:
Definition of the imaginary unit ![]() : The imaginary unit
: The imaginary unit ![]() is the number whose square is equal to
is the number whose square is equal to ![]() . That is,
. That is,
(5) ![]()
In other words, the imaginary unit ![]() is the solution of the quadratic equation
is the solution of the quadratic equation
(6) ![]()
Here, we should keep in mind that ![]() is also the solution of this quadratic equation, this is because
is also the solution of this quadratic equation, this is because
(7) 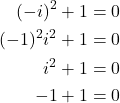
Let us now explain how to compute the powers of ![]() . We have
. We have
(8) 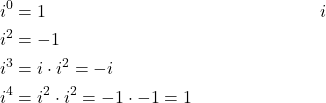
It is easy to see that after ![]() , the pattern repeats. That is we have
, the pattern repeats. That is we have
(9) 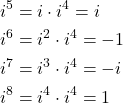
This pattern repeats itself with the period of ![]() . That is
. That is
(10) ![]()
Now, that we understand the imaginary unit, we can formally define the complex numbers.
Definition of complex numbers: Complex numbers are numbers having the following form
(11) ![]()
where
For example, the number
(12) ![]()
is the complex number with the real part of ![]() and with the imaginary part of
and with the imaginary part of ![]() . The imaginary unit
. The imaginary unit ![]() is a complex number with the real part of
is a complex number with the real part of ![]() and with the imaginary part of
and with the imaginary part of ![]() .
.
Notation for real and imaginary parts of complex numbers. Usually, we use the letter ![]() to represent complex numbers. That is,
to represent complex numbers. That is, ![]() . Then, we can introduce the following notation. The notation
. Then, we can introduce the following notation. The notation ![]() denotes the real part of the complex number. That is,
denotes the real part of the complex number. That is, ![]() . The notation
. The notation ![]() denotes the imaginary part of the complex number. That is,
denotes the imaginary part of the complex number. That is, ![]() .
.
Graphical Interpretation of Complex Numbers
The complex numbers can be represented graphically like this:
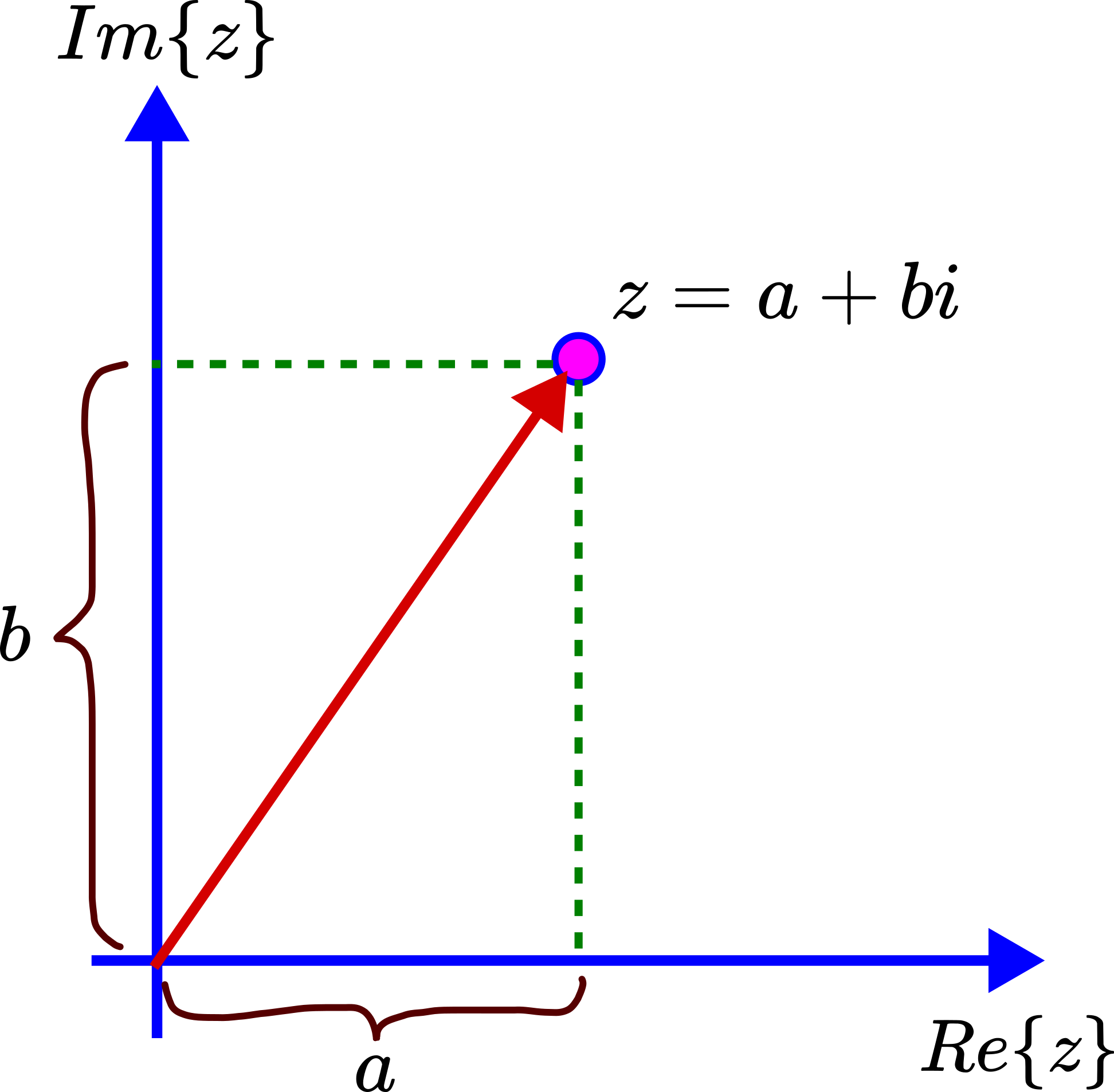
The complex number ![]() can be represented as a point in the 2D plane. The horizontal axis is used to represent the real part of the complex number
can be represented as a point in the 2D plane. The horizontal axis is used to represent the real part of the complex number ![]() . The vertical axis is used to represent the imaginary part of the complex number
. The vertical axis is used to represent the imaginary part of the complex number ![]() . Then, the complex number
. Then, the complex number ![]() can be interpreted as a point in the 2D plane determined by the axes
can be interpreted as a point in the 2D plane determined by the axes ![]() and
and ![]() . The coordinates of
. The coordinates of ![]() are then
are then ![]() .
.
Basic Operations with Complex Numbers
In this section, we explain how to perform basic operations with complex numbers.
But first, we need to provide the answer to the following question:
Given two complex numbers ![]() and
and ![]() , when are these two complex numbers equal?
, when are these two complex numbers equal?
ANSWER: Two complex numbers are equal if they have equal real and imaginary parts. That is, if ![]() and
and ![]() , then
, then
(13) ![]()
Sum of complex numbers: Let ![]() and
and ![]() be two complex numbers. Then, the sum of the complex numbers is
be two complex numbers. Then, the sum of the complex numbers is
(14) ![]()
That is
(15) ![]()
Difference of Complex Numbers:Let ![]() and
and ![]() be two complex numbers. Then, the difference of the complex numbers is
be two complex numbers. Then, the difference of the complex numbers is
(16) ![]()
That is
(17) ![]()
Product of Complex Numbers: There is a formula for the product of complex numbers. However, you do not need to remember this formula since you can easily derive it. In fact, you do not need to know this formula, you can manually multiply the complex numbers. Let ![]() and
and ![]() be two complex numbers. Then, we have
be two complex numbers. Then, we have
(18) 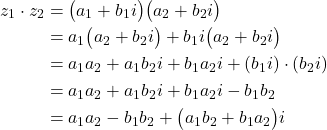
Another important concept that we need to introduce is the concept of the conjugate of a complex number. This concept is introduced in the sequel.
Conjugate of a complex number: Let ![]() be a complex number. Then its conjugate is denoted by
be a complex number. Then its conjugate is denoted by ![]() and is defined as follows
and is defined as follows
(19) ![]()
In other words, the complex number and its conjugate have equal real parts and the imaginary parts have opposite signs.
Also, in books and in papers, you will also see a bar over a complex number. For example if you see ![]() this is computed as follows
this is computed as follows
(20) ![]()
That is, the overline notation denotes the conjugate operation performed on the complex number.
To practice complex number operations, let us do two examples.
Example 1: Calculate the complex number expression
(21) 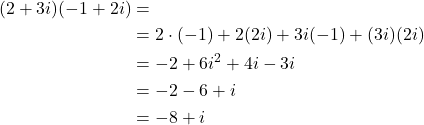
Example 2: Calculate the complex number expression
(22)